


Next: 4.5 Integration into a
Up: 4. Optimizer
Previous: 4.3.6 Model Library
4.4 General Nonlinear Optimization Problems
General nonlinear optimization problems have a slightly different
structure than the least-squares problems discussed in the previous section.
Here the cost function 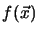 should be
minimized. For doing this the optimizer can vary the parameter vector
should be
minimized. For doing this the optimizer can vary the parameter vector
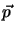 within the defined boundaries.
within the defined boundaries.
In this general description of the problem it can occur that a
numerically optimal solution lies within a nonphysical area. For this
reason the feasible area has to be reduced. This is done by so called
inequality and equality constraints.
Figure 4.4:
Structure of a general nonlinear
optimization problem with equality and inequality constraints.
|
![\resizebox{6.cm}{!}{
\psfrag{Model}{Model}
\psfrag{M}{$\mathcal{M}$}
\psfrag{...
...f}{Target Function $f$}
\includegraphics[width=6.cm]{graphics/gnostruct.eps}
}](img179.gif)
|
The solution of a general nonlinear optimization problem is found
using the package donlp24.5 in which the following steps are processed.
- 1. Choose a value
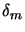
- 2. From all inequality constraints, only those are selected which are nearly active
(
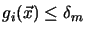 ).
).
- 3. Solve the quadratic problem built by the gradient and Hessian of
the target function subject to a reduced set of inequality
constraints and all equality constraints. The Hessian was built by
a BFGS-update described in Section 4.1.6. The result is the
step direction and the slack variables u and v.
- 4. Check for termination
- 5.
If the calculated step is to small or the violation of the constraints exceed tau0 then
increase
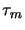 and go to step 3
else proceed.
and go to step 3
else proceed.
- 6. Compute new penalty weights
- 7. Select the step size
- 8. Assign a new value for x and
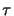 and resume at step 1
and resume at step 1
Footnotes
- ...donlp24.5
- Further details of the algorithm can be
found in [49,50] or in the documentation of the
program in [51].



Next: 4.5 Integration into a
Up: 4. Optimizer
Previous: 4.3.6 Model Library
R. Plasun
![]() should be
minimized. For doing this the optimizer can vary the parameter vector
should be
minimized. For doing this the optimizer can vary the parameter vector
![]() within the defined boundaries.
within the defined boundaries.
![\resizebox{6.cm}{!}{
\psfrag{Model}{Model}
\psfrag{M}{$\mathcal{M}$}
\psfrag{...
...f}{Target Function $f$}
\includegraphics[width=6.cm]{graphics/gnostruct.eps}
}](img179.gif)