To solve complex differential equation systems it is necessary to divide the domain of interest into a number of subdomains or elements. Once the concept of subdividing a physical domain into elements is accepted the problem of analyzing a variation of a variable across the whole domain becomes far easier, since the variation can be related with each single element. If such an approximation across an element is defined and since elements are interconnected, it is a simple matter that the variation across the whole domain has, in a piecewise manner, been effected.
The shape functions are a means of interpolation of the discrete nodal
variables. In general they are set up in a local coordinate system
(
![]() ,
,![]() ,
,![]() ) which implies an element transformation from global
coordinates to local ones. In comparison to other discretization
methods it seems to be an overhead to transform a general element
located in the (x,y,z)-system to a standard element defined in a local
coordinate system (
) which implies an element transformation from global
coordinates to local ones. In comparison to other discretization
methods it seems to be an overhead to transform a general element
located in the (x,y,z)-system to a standard element defined in a local
coordinate system (
![]() ,
,![]() ,
,![]() ). At closer inspection this
transformation turns out to enable necessary integrations over an
element to be performed with ease. Furthermore, a generalized
methodology can be defined offering the possibility to solve complex
PDE systems on various elements with different interpolation orders
and dimensions without necessity to change the underlying concept.
). At closer inspection this
transformation turns out to enable necessary integrations over an
element to be performed with ease. Furthermore, a generalized
methodology can be defined offering the possibility to solve complex
PDE systems on various elements with different interpolation orders
and dimensions without necessity to change the underlying concept.
To perform finite element analysis the matrices defining element
properties have to be found. They will always be of the form
| (3.6) |
Since the values of ![]() are only defined on discrete points of
an element a variation of the function has to be chosen. This is
normally done using (3.3) and introducing N as a
shape function of choice (see Appendix B).
are only defined on discrete points of
an element a variation of the function has to be chosen. This is
normally done using (3.3) and introducing N as a
shape function of choice (see Appendix B).
With these definitions (3.7) can be written as
| (3.8) |
Galerkin's approach suggests to use weighting functions w that are
set to be equal to the shape functions N (wj = Nj with j = 1,2,
... ,m). Because N only depends on the global coordinates (x,y,z) (3.7) can now be transformed to
| (3.9) |
| (3.10) |
It is remarkable that two transformations are necessary to evaluate this integral over the domain of interest:
To express these transformations, consider a set of local
coordinates (
![]() ,
,![]() ,
,![]() ) and a corresponding set of global
coordinates (x, y, z). By the rules of partial differential
equations the derivatives of the shape functions have the form
) and a corresponding set of global
coordinates (x, y, z). By the rules of partial differential
equations the derivatives of the shape functions have the form
| (3.12) | |||
| (3.13) | |||
| (3.14) |
The left-hand side of (3.15) depends only on the shape functions Ni that are specified in the local coordinate system. Furthermore, as (x, y, z) are given explicitly, the matrix J can be found in terms of local coordinates. This matrix is known as the Jacobian matrix.
Since the point of interest is the definition of derivatives in terms of
locally defined shape functions the remaining task is to convert the
Jacobian matrix J. As a result the derivatives of the shape
functions in the general coordinate system are found to be:
| (3.16) |
For integration purposes a general located element defined in the
spatial coordinates (x, y, z) is mapped onto a standard element
in the (
![]() ,
,![]() ,
,![]() ) coordinate system (Fig. 3.2). Again
the variation approach can be used but now interpolating the
coordinate vectors itself instead of a distributed value. The
variation approach can be written as
) coordinate system (Fig. 3.2). Again
the variation approach can be used but now interpolating the
coordinate vectors itself instead of a distributed value. The
variation approach can be written as
det 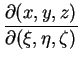
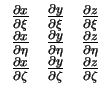
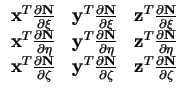
|
(3.18) |
det 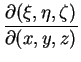
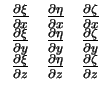
|
(3.19) |
To transform the variables and the region with respect to which the
integration is made a standard process will be used that also
involves the determinant J. Thus a volume element becomes
| dx dy dz = det |
(3.20) |
Assuming that the inverse of J can be found the problem of
general evaluation of an integral (see also Section 3.1.2) is now reduced to element properties
![]() of the form
of the form
The integration is carried out within a standard element in the local coordinate system and not in the complicated distorted shape, thus accounting for the simple integration limits. Similar one- and two-dimensional problems will result in integrals with one or two coordinates within simple limits, since the complete concept is valid independent of the dimension used.
While the limits of the integration are simple, unfortunately the
explicit form of
![]() (
(![]() ,
,![]() ,
,![]() ) is not. Non standard
algebraic integration usually defies the mathematical average skill,
and numerical integration has to be resorted to. This, as will be seen
in the next section, is not a severe penalty and has the advantage
that the solution is not tied to a particular element or partial
differential equation but can be written for various classes of
problems.
) is not. Non standard
algebraic integration usually defies the mathematical average skill,
and numerical integration has to be resorted to. This, as will be seen
in the next section, is not a severe penalty and has the advantage
that the solution is not tied to a particular element or partial
differential equation but can be written for various classes of
problems.