Die Boundary Element Methode (BEM) gehört zu den randorientierten
Diskretisierungsmethoden, das bedeutet, dass sie mit einem Gitter am Rand
des Simulationsbereiches auskommt und keine Gitterpunkte im Inneren benötigt.
Diese Methode ist allerdings nur dann anwendbar, wenn die Fundamentallösung
der Differentialgleichung bekannt ist.
Beispielsweise geht man bei der Berechnung des elektrischen Feldes davon aus,
dass elektrische Ladungen ausschließlich auf der Oberfläche der Elektroden
vorhanden sind.
Das elektrische Potenzial an einem Punkt
![]() lässt sich dann als
Integral über alle elektrische Ladungen (auf den Oberflächen aller Leiter
lässt sich dann als
Integral über alle elektrische Ladungen (auf den Oberflächen aller Leiter
![]() ) berechnen:
) berechnen:
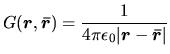 |
(3.2) |
Sind mehrere Materialien mit unterschiedlichen Dielektrizitätszahlen vorhanden, ist es meist schwierig die dazu passende Green'sche Funktion zu finden. Beispielsweise lässt sich für mehrere ebene Lagen unterschiedlicher Materialien die Green'sche Funktion durch ,,Spiegelladungen`` [85] oder durch ein Fourier-Integral ermitteln [86].
Allgemeine Geometrien kann man mit der BEM nur berechnen, indem man sämtliche Materialgrenzen ebenfalls mit Randelementen diskretisiert, um die dort auftretende Polarisationsladung zu berücksichtigen. Systeme mit einer großen Anzahl von Materialgrenzen sowie homogenen Neumann-Bedingungen lassen die Ordnung des Gleichungssystems schnell ansteigen und die Effizienz dieses Verfahrens sinkt. Inhomogene und nichtlineare Materialien können mit der Boundary Element Methode überhaupt nicht berechnet werden. Eine Begrenzung des Simulationsgebietes nach außen (so wie bei der FDM und FEM) ist nicht erforderlich, da durch die Green'sche Funktion implizit die Wirkung des elektrischen Feldes bis ins Unendliche enthalten ist.
Um den Rechenaufwand zur Lösung des Gleichungssystems zu verkleinern, kann man die Einflüsse zweier weit entfernter Gruppen benachbarter Randelemente zusammenfassen indem man deren Green'sche Funktionen mittels Multipol-Expansion bzw. einer Taylor-Reihe annähert und dadurch eine Reduktion der Systemmatrix erreicht [87,88]. Es besteht aber auch die Möglichkeit die Einflüsse von sehr weit entfernten Elementen derart zu vernachlässigen, dass an diesen Stellen in der inversen Systemmatrix keine Kopplungen auftreten und Bandstruktur erreicht wird. Damit kann der Aufwand zur Lösung reduziert werden (Schur-Inversion [89]). Eine weitere Reduktion des Rechenaufwandes lässt sich erzielen, indem man die Integration der Green'schen Funktion durch eine numerische Näherung basierend auf einer Multipol-Expansion beschleunigt [90,91]. Mittels Eigenwertzerlegung [92,93], Wavelet-ähnlichen Methoden [94] oder auf FFT basierenden Verfahren [95] kann man ereichen, dass die Besetzungsdichte der Systemmatrix reduziert und iterative Lösungsverfahren somit beschleunigt werden. Singularitäten der Green'schen Funktion verkomplizieren die Integration, doch oft lassen sich für die singulären Integrale analytische Lösungen finden [96,97].
Die Boundary Element Methode wird bevorzugt zur Kapazitätsberechnung eingesetzt [98,99,100,101,102], aber auch zur Berechnung von Substratwiderständen [103,104], da hier keine unregelmäßigen Neumann-Bedingungen auftreten.