Das Auffinden des nächsten Gitter- bzw. Geometriepunktes oder das
Feststellen in welcher Gitterzelle bzw. in welchem Solid sich ein
vorgegebener
Punkt befindet ist eine Prozedur, die bei vielen geometrischen Operationen
als Teilschritt enthalten ist.
Wie schon oben erwähnt, ist diese Aufgabe bei CSG-Geometrien sehr
einfach zu implementieren.
Ebenso bei Ortho-Produkt-Gittern--die Suche kann hier für jede
Koordinatenachse getrennt durchgeführt werden (am effizientesten mittels
binärem Suchen).
Bei allgemeinen strukturierten Gittern, unstrukturierten Gittern
sowie BRep Geometrien ist ein effizientes Suchverfahren in der
Implementierung deutlich aufwendiger.
Natürlich ist es möglich, alle Zellen des Gitters bzw. alle Solids der
Geometrie nacheinander zu prüfen, ob der gesuchte Punkt enthalten ist.
Da die Tests, ob ein Punkt innerhalb eines bestimmten Körpers ist, relativ
aufwendig sind, hat diese Methode auch einen großen Bedarf an CPU-Zeit.
Man kann zwar mittels sogenannter Boundingbox-Tests eine deutliche
Geschwindigkeitssteigerung erzielen, jedoch bleibt der Rechenaufwand bei
einer Größenordnung von 
.
Hingegen erreichen Verfahren, die mit einem Suchbaum arbeiten in der Regel
einen Aufwand von 
.
Nach dem gleichen Prinzip wie ein binärer Baum für eindimensionale Daten arbeitet der Punkt-Octree (oder auch Point-Bucket-Octree) bei der Suche nach Geometriepunkten in drei Dimensionen. Jeder Knoten des Octrees entspricht einem Würfel (bzw. Quader) und wird durch seine Kinder in acht Würfel mit der halben Seitenlänge aufgeteilt (Abb. 5.7). Die Wurzel des Baumes bildet ein Würfel, der das gesamte darzustellende Gebiet umschließt.
|
Neben dem Suchen nach vorhandenen Punktkoordinaten kann man den Punkt-Octree
auch zum Auffinden von Punkten in einem vorgegebenen Bereich, Suchen des
nächstgelegen Punktes und ähnlichen Operationen verwenden.
Der Aufwand dieser Operationen beträgt unter der Voraussetzung,
dass der Octree zumindest einigermaßen balanciert ist, ansonsten
kann er zu ausarten.
Da die Flächen des Octrees parallel zu den Koordinatenachsen sind, können
Vergleiche, ob Punkte in einem Würfel liegen oder nicht, für die
, 
, und 
-Koordinaten exakt durchgeführt werden, und man braucht
keine Abstände oder Schnitte zu berechnen, was zu numerischen Ungenauigkeiten
führen könnte.
Mir einem erweiterten Octree (auch Finite Octree) [127] lassen sich nicht nur die Punkte, sondern auch die Linien, Flächen und Solids einer Struktur geometrisch ordnen. Er eignet sich deshalb zur Suche von Objekten in unstrukturierten Gittern oder BRep-Geometrien. Wie beim Punkt-Octree wird der Raum in Würfel eingeteilt, wobei jeder Würfel in acht Sub-Würfel aufgeteilt wird, bis ein Grenzkriterium erreicht wird. Abbildung 5.8 zeigt die vier möglichen Fälle, bei denen die Aufteilung abgebrochen wird, da ein weiteres Zerlegen des Würfels mindestens einen Sub-Würfel des selben Typs hätte. Einen Knoten, der nicht weiter zerteilt wird, nennt man Blatt.
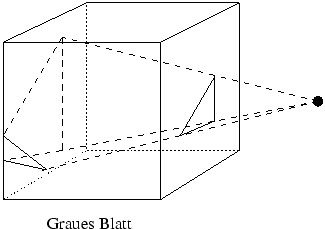
Im Fall, dass ein Geometrie-Punkt sehr nahe an einer Teilungsebene des Octrees liegt, und zwei Linien oder Flächen, die in einem sehr spitzen Winkel zueinander stehen, diese Ebene durchstoßen, ist der Abstand der Durchtrittspunkte(-linien) sehr klein. Er kann sogar kleiner als die Auflösung der im Rechner darstellbaren Zahlen werden, was zur Folge hat, dass dieser Fall nicht im Octree darstellbar ist, da nicht mehr weiter unterteilt werden könnte. Um dies zu verhindern wird ein neuer Blatt-Typ eingeführt (Graues Blatt). Sein Aufbau (siehe Abb. 5.9) ist ähnlich dem Punkt-Blatt mit der Ausnahme, dass sich der Punkt außerhalb des Blattes befinden darf, alle Flächen und Linien innerhalb des Blattes müssen jedoch diesen Punkt enthalten.
|
Ob sich ein Punkt in einem bestimmten Octree-Würfel befindet oder nicht,
kann wie zuvor durch direkten Koordinatenvergleich herausgefunden werden.
Schwieriger ist es zu bestimmen, ob eine Linie oder Fläche einen Würfel
schneidet.
Zwar gibt es dafür einfache Testverfahren, doch muss dabei
unbedingt darauf geachtet werden, dass es nicht etwa durch numerische
Ungenauigkeiten zu inkonsistenten Ergebnissen kommt.
Es ist deshalb ratsam ein Verfahren zu wählen, dass auf Punktvergleichen
basiert, da diese exakt durchgeführt werden können.
Die Aufgabe kann also folgendermaßen formuliert werden:
Finde einen Punkt, der falls die Fläche (Linie) den Würfel schneidet,
mit Sicherheit innerhalb des Würfels liegt.
Ein solcher Punkt kann durch Schnitt mit den Raumdiagonalen (
)
bzw. mit den Diagonalebenen (
, 
, 
) des
jeweiligen Würfels gefunden werden.
Da benachbarte Würfel Raumdiagonalen und Diagonalebenen gemeinsam haben,
ist garantiert, dass auch die Schnittfunktionen ungeachtet numerischer
Ungenauigkeiten das gleiche Ergebnis liefern und Konsistenz gewährleistet
ist.
Neben dem beschleunigten Suchen nach Geometrieelementen kann ein erweiterter Octree auch effizient zur Kollisionserkennung, Gittererzeugung [128,129], Voxel-Diskretisierung und Booleschen Operationen (siehe unten) verwendet werden.
|
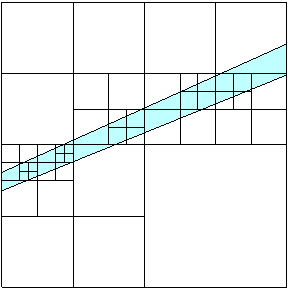
Da bei einem Octree immer an vordefinierten Stellen parallel zu den Koordinatenebenen unterteilt wird, kann es bei stark nichtsymmetrischen Geometrien vorkommen, dass der Baum nicht gut balanciert ist, was die Leistungsfähigkeit beim Suchen verringert. Auch bei der Darstellung dünner Schichten, die nicht parallel zu den Achsen sind, kommt es zu Leistungseinbußen, da hier so oft verfeinert werden muss, bis die Grenzflächen in verschiedenen Würfeln liegen (Abb. 5.10). Diese Nachteile lassen sich durch den BSP-Baum (Binary Space Partitioning) beheben. Die Wurzel dieses Baumes repräsentiert den gesamten Raum. Jeder Knoten hat (nicht wie beim Octree acht, sondern) genau zwei Kinder, die durch Teilung mittels einer Ebene entstehen. Als Teilungsebenen verwendet man Flächen der Geometrie und wählt diese so aus, dass ein (annähernd) balancierter Baum entsteht. Das Aufteilen wird abgebrochen, wenn ein Blatt des Baumes ausschließlich in einem einzigen Solid liegt. Der BSP-Baum bildet somit einen Übergang von der BRep- zur CSG-Darstellung.
