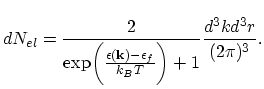For a system of particles described by antisymmetric wave functions the Pauli exclusion principle implies that only one particle can be placed at each
quantum state. To derive the distribution function the Gibbs distribution is applied to the subsystem of particles which are in the same quantum state.
This is possible even in the presence of the exchange interaction because it only takes place inside the subsystem. Taking into account that the energy is
equal to
 the thermodynamic potential is given as:
the thermodynamic potential is given as:
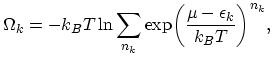 |
(2.27) |
where  stands for all quantum numbers characterizing the particle state,
stands for all quantum numbers characterizing the particle state, 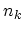 is the number of particles in state
is the number of particles in state 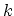 and
and 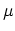 is the chemical
potential of the system2.6. According to the Pauli exclusion principle occupation
numbers
is the chemical
potential of the system2.6. According to the Pauli exclusion principle occupation
numbers 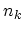 for fermions can only take values 0 or
for fermions can only take values 0 or 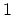 . Thus the thermodynamic potential has the form:
. Thus the thermodynamic potential has the form:
![$\displaystyle \Omega_{k}=-k_{B}T\ln\biggl[1+\exp\biggl(\frac{\mu-\epsilon_{k}}{k_{B}T}\biggr)\biggr].$](img207.png) |
(2.28) |
Since the average number of particles is defined through the derivative of the thermodynamic potential (2.28), with respect to the chemical
potential 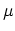 by the expression:
by the expression:
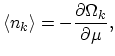 |
(2.29) |
the expression for the average fermion number in state 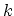 is:
is:
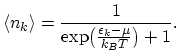 |
(2.30) |
It can be seen from (2.30) that all
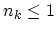 and when
and when
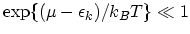 the Boltzmann distribution function2.7 is obtained. The
normalization is obtained from the condition that the sum over all
the Boltzmann distribution function2.7 is obtained. The
normalization is obtained from the condition that the sum over all
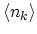 is equal to the total number of particles
is equal to the total number of particles 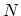 in the system:
in the system:
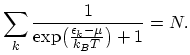 |
(2.31) |
The normalization condition gives the chemical potential 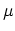 as an implicit function of the temperature
as an implicit function of the temperature 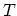 and the total number of particles
and the total number of particles 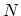 in
the system.
in
the system.
For example, for the equilibrium electron gas in solids the number of electrons in the phase space element
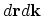 can now be written
as2.8:
can now be written
as2.8:
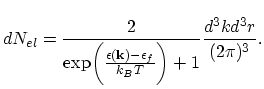 |
(2.32) |
The physical meaning of the Fermi energy is that it is the largest electron energy at zero temperature. It is a boundary between occupied and free states.
At non-zero temperatures electrons can also occupy states above the Fermi energy as shown in Fig. 2.4.
Figure 2.4:
The Fermi-Dirac distribution at zero and finite temperatures.
|
|
S. Smirnov:
![]() can now be written
as2.8:
can now be written
as2.8: