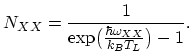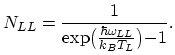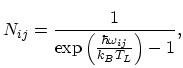Subsections
An electron can be scattered from one valley to another one both by acoustical and optical phonons. Intervalley scattering can be treated as a
deformation-potential interaction [30] in the same way as intravalley scattering by optical phonons.
This scattering process is subdivided into f-type and g-type processes. A process is referred to as f-type, if the initial and final orientations are
different, otherwise as g-type process. The transition probability of this mechanism is given by:
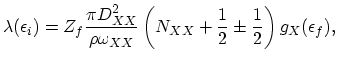 |
(2.115) |
where
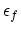 is:
is:
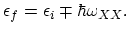 |
(2.116) |
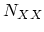 is the equilibrium phonon number of the involved phonon type:
is the equilibrium phonon number of the involved phonon type:
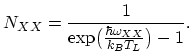 |
(2.117) |
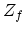 is the number of possible equivalent final valleys of the same type. For f-type scattering
is the number of possible equivalent final valleys of the same type. For f-type scattering 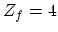 and for g-type scattering
and for g-type scattering 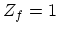 .
.
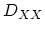 is the coupling constant,
is the coupling constant,
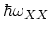 is the corresponding phonon energy.
is the corresponding phonon energy.
The numerical values of the coupling constants and phonon energies [18,20] are shown in Table 2.4.
For this type of scattering there is no separation into f- and g-type processes. The scattering rate is given as:
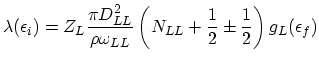 |
(2.118) |
where
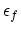 is
is
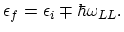 |
(2.119) |
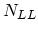 is the equilibrium phonon number of the involved phonon type:
is the equilibrium phonon number of the involved phonon type:
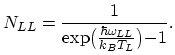 |
(2.120) |
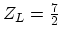 for the transition between two different orientations and
for the transition between two different orientations and
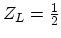 for scattering within the
same orientation,
for scattering within the
same orientation, 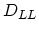 denotes the corresponding coupling constant and
denotes the corresponding coupling constant and
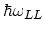 is the energy of the phonon involved in the scattering
process.
is the energy of the phonon involved in the scattering
process.
The numerical values of the coupling constants and phonon energies [18,20] for this type of scattering are shown in Table 2.5.
This process involves transitions between all possible valleys in the conduction band. The scattering rate is given by:
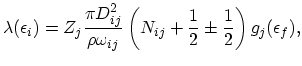 |
(2.121) |
where
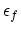 is:
is:
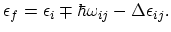 |
(2.122) |
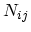 is the equilibrium phonon number of the involved phonon type:
is the equilibrium phonon number of the involved phonon type:
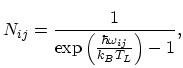 |
(2.123) |
and
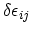 is given as
is given as
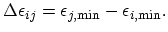 |
(2.124) |
Indices 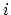 and
and 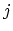 stand for the initial and final valley, respectively,
stand for the initial and final valley, respectively, 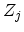 is the number of possible equivalent final valleys,
is the number of possible equivalent final valleys, 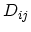 is
the corresponding coupling constant,
is
the corresponding coupling constant,
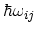 is the respective phonon energy,
is the respective phonon energy,
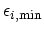 and
and
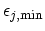 are the energy
minima of the initial and the final valley, respectively.
are the energy
minima of the initial and the final valley, respectively.
The numerical values of the coupling constants and phonon energies [18,20] for this type of scattering are shown in Table 2.6.
S. Smirnov: