|
|
|
|
||
| Previous: 3.5.1 Electron-Phonon Scattering Up: 3.5 Scattering Mechanisms in Strained SiGe Next: 3.5.3 Plasmon Scattering | ||||
For an analytical band structure taking into account nonparabolicity and anisotropy the density of states of one valley is given by
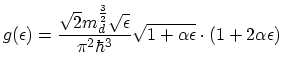 |
(3.67) |
Including nonparabolicity up to the second order the contribution of valley ![]() with orientation
with orientation ![]() to the inverse screening length takes the following
form:
to the inverse screening length takes the following
form:
It should be noted that in semiconductors with non-parabolic bands the inverse screening length increases which may weaken the ionized impurity scattering rate in particular for a high doping level when due to the Pauli exclusion principle the population of higher energies increases significantly. Thus there are two opposite factors which determine the strength of ionized impurity scattering. Another interesting effect occurs in strained doped materials. Due to strain some valleys shift up and do not contribute to the kinetics. However, this may change at high degeneracy when the Pauli principle causes the upper split bands to be populated, which then also give a contribution to the transport properties. The repopulation may be significant leading to a reduction of the valley splitting effect.
In case of momentum-dependent screening the dielectric function is modified to take into account the strain induced splitting of the conduction band minima for different valleys and orientations:
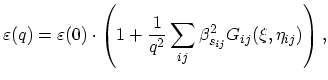 |
(3.70) |