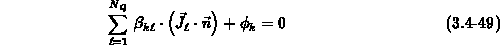
For the discretization of the boundary conditions (3.4-49) it is, from a physical perspective, crucial to evaluate the flux component perpendicular to the boundary consistently and accurately.
Let us take a closer look at the transformed boundary conditions, e.g. for
the north boundary 
(3.4-50).
We easily identify the term 
which we had defined for the discretization
of the divergence. The flux through the north/south boundary then is
(3.4-51) and the expression for the flux through the west/east
boundary reads (3.4-52).
Considering an element at the north boundary (Figure 3.4-6), the
divergence expression for the boundary point 
has the form
(3.4-53), with the yet unknown contribution 
. We
define an incomplete divergence expression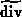 
just
omitting the unknown value 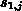(3.4-54). The
corresponding expressions for the other boundaries are self-evident.
When the continuity expression (3.4-55) is fulfilled, we are
able to calculate the missing term 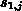from the
residual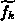 
(3.4-56) using the incomplete
divergence. Thus, the fluxes we need for the boundary conditions are given
by (3.4-57), (3.4-58). The weighting factors
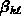for the individual fluxes are constant. They are the only
coefficients in the PDEs which must not depend on the concentrations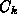 
.
The handling of the term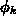 
in the boundary conditions is obvious. It
is an additional term just like the recombination term
(Chapter 3.4.4) which is added unaltered to the discretized
equation. Certainly, 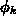may depend on the local concentration at the
boundary, just considering Dirichlet type boundary conditions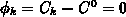 
. But 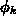may depend on the concentration at the first
point inside the simulation domain (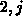
in Figure 3.4-6) as
well. This dependency allows the treatment of one-dimensional artificial
infinite boundary elements [Mar82], [Mar83]. Such infinite
elements are very useful for artificial device boundaries in order to keep
the simulation domain small. Nevertheless, we dissuade from excessive
application of this technique, since its extension to the two-dimensional
nonplanar case is not at all straightforward.
In the conservative transformation of the time derivatives
(3.3-57) we included the effect of the moving grid points in a
divergence term and hence in the discretization of the flux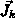 
.
The way how boundary conditions are interpreted in the case of moving
boundaries is a consequence of this extended flux definition and the
boundary flux calculation (3.4-57),
(3.4-58). Figuratively speaking, the boundary conditions are
defined by an observer sitting at the boundary. An impermeable
boundary is thus described by 
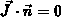, regardless of any
boundary motion.
