| div( |
(3.31) |
In contrast to the finite element discretization, which is a general
mathematical motivated approach to solve complex differential equation
mapped on a discretized simulation domain, the finite boxes are more
physically motivated and especially in problems where a conservative
law
| div( |
(3.31) |
The idea is to calculate the flux across a defined volume using Gauss'
integration method
The integral (3.32) can be discretized with
| (3.33) |
The flux itself can be approximated by finite differences
Fij  |
(3.34) |
To calculate the sum in (3.35) the geometric coefficients Ai denoting the coupling cross section and lij which is the distance between the two corresponding discrete points [Fis94a] have to be found.
|
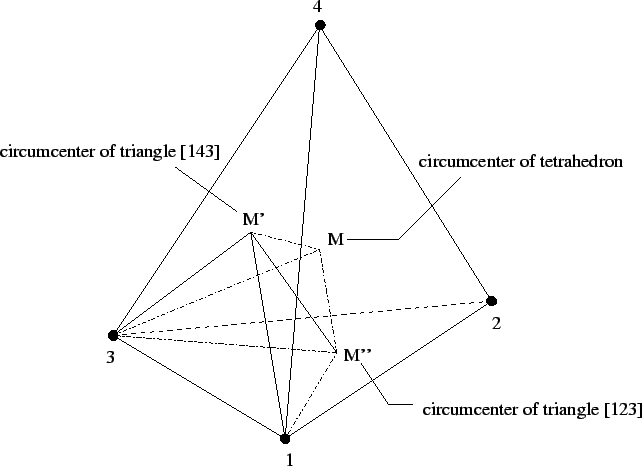
The same procedure can be used calculating the discretization for three-dimensional problems where just the geometrical operations are more complicated than in the two-dimensional case [Mil94]. To meet the element-wise approach of finite elements the box can be calculated using the circumcenter M of the tetrahedron and the circumcenters of the triangular faces (Fig. 3.6). A Voronoi box in the three-dimensional case can be calculated by adding the resulting subtetrahedrons of all elements linked to a single point.
Due to the simple mapping mechanism between physics and discretization the finite box integration has been used very successfully in describing rather complex physical models such as semiconductor equations [Sim96] or coupled diffusion equations [Lei97].