

Next: 4.3.1.7 Miscellaneous Features
Up: 4.3.1 The Model Definition
Previous: 4.3.1.5 Parameters
4.3.1.6 Auxiliaries
A very useful feature of AMIGOS is the definition of auxiliary
variables. These variables are treated like quantities but are solved
explicitly which reduces the amount of memory and calculation
time. Explicit means, that they are not involved in the Newton
iteration step solving the global stiffness matrix but they build a
subsystem of their own which is defined by the interconnections of the
nearest element neighbors of the mesh (Fig. 4.3.1.6).
AMIGOS automatically detects the dimension of the auxiliary variable that might
be an n-dimensional tensor, and writes its output as separate
result value to a file for later reuse or visualization.
Figure 4.5:
Auxiliary calculation depending on element interconnections and weighting function
Aux U = grad(A);
# defines U as auxiliary
# to calculate a gradient
# field of quantity A
Aux Vol = V/3;
# defines Vol as auxiliary
# for later use as weighting
# function
|
|
To meet all requirements of different auxiliary types there are
several update modes that have already been introduced in the section
about the Input & Control Interface (4.2). The following
list shows the different modes and their calculation methods
referring to Fig. 4.3.1.6 where U is a derived gradient
field of the quantity A weighted by the volume of the surrounding
elements corresponding to point 0 (e.g. volume might be a Voronoi box):
- if the user does not specify the type of update mode in the
Input & Control Interface the default formula
Aux U = 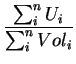 |
|
|
(4.4) |
will be used to calculate the auxiliaries.
- update Newton-like initializes the auxiliary U to be updated
in the same manner as a quantity calculated by a Newton iteration
where the used formula is
Aux U = 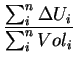 |
|
|
(4.5) |
- update after timestep initializes the auxiliary U to be updated
after finishing a time step integration. This means, that during the
time-step calculation the auxiliary U is treated as a constant
value. The used formula is the same as in (4.4).
- update after timestep but Newton-like handles the auxiliary U as
described in the previous point but using the calculation
after (4.5).
- explicit moving grid integration offers the possibility to write
a calculated auxiliary variable to the coordinate vectors. In this
case the auxiliary must be a vector of the size of element points and
after each time-step the coordinates of each element are updated to the
new value calculated during solving the total system.


Next: 4.3.1.7 Miscellaneous Features
Up: 4.3.1 The Model Definition
Previous: 4.3.1.5 Parameters
Mustafa Radi
1998-12-11