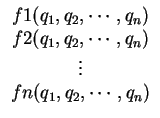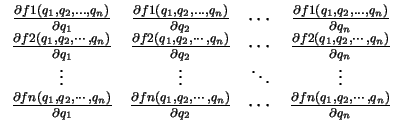

Next: 4.4.2 Boundary Models
Up: 4.4 Assembling of the
Previous: 4.4 Assembling of the
A lot of partial differential equations can be discretized so that
finally a sparse matrix results which represents a linear equation
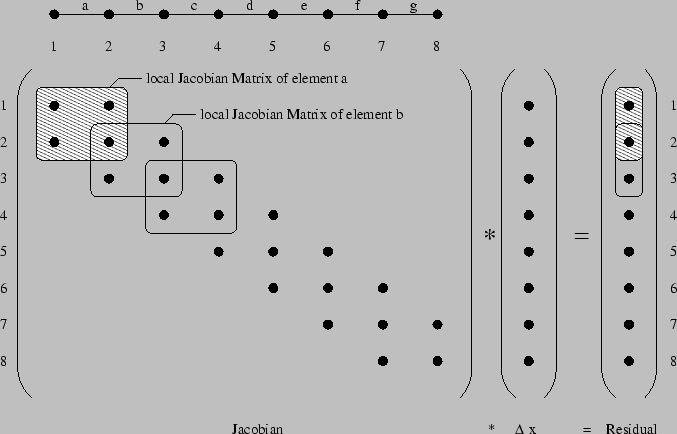
system that has to be solved (Fig. 4.9). In case of non
linearity an iteration is necessary where successive approximations are
calculated. The condition for the nonlinear system
is satisfied in case of
lim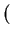 xi xi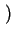 = xs
= xs |
|
|
(4.7) |
Looking at the first order of the Taylor series
f (xs) = f (xi) + 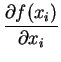 . .  xs - xi xs - xi + O
+ O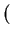 xs - xi xs - xi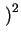 = 0
= 0 |
|
|
(4.8) |
it is obvious that in case of a linear approximation where terms of higher order are neglected (
O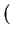 xs - xi
xs - xi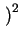 = 0) the resulting linear equation system
= 0) the resulting linear equation system
F(xi) . 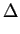 xi + f (xi) = R xi + f (xi) = R |
|
|
(4.9) |
satisfies the postulated condition when
R  0. In case of linear
systems the solution can immediately be determined by
0. In case of linear
systems the solution can immediately be determined by
xi + 1 = xi + 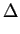 xi = xs xi = xs |
|
|
(4.10) |
The vector f(x) denotes the so called Residual function
which is a vector of functions of the searched quantities
q1, q2, ... , qn.
Its derivative stands for the system matrix or also called Jacobian Matrix and can be calculated using the following rule
AMIGOS uses this mathematical expression profitably so that an
automatic assembling of the global stiffness matrix is done depending
on the basis of a discretized simulation domain. It simplifies the
task of global assembling of all grid points and reduces it to a local
process where the PDE system has to be discretized only on a single
element. To preserve one's survey it is much easier to handle just
the smaller local part of the discretization than dealing with
the global assembling step (Fig. 4.9). Furthermore,
AMIGOS releases the model developer from the duty to calculate the
Jacobian matrix using its derivative operator that derives
the residual function symbolically.
Figure 4.9:
Auto assembling mechanism of a one-dimensional simulation domain
with linear two point elements
|
|


Next: 4.4.2 Boundary Models
Up: 4.4 Assembling of the
Previous: 4.4 Assembling of the
Mustafa Radi
1998-12-11
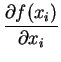 .
.