|
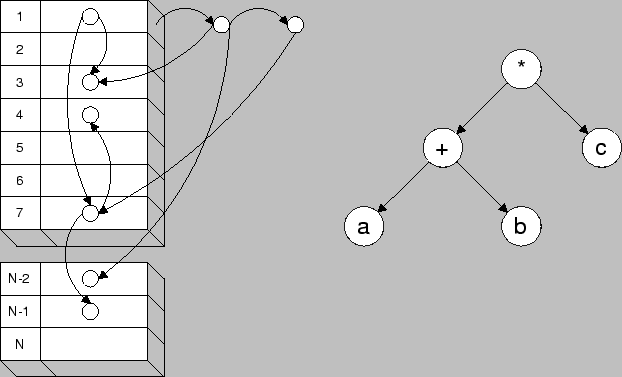
The Analytical Model Interface is designed in a way that every mathematical expression is represented with a tree structure that is assembled into an extendible hash shown in Fig. 5. The hash table is used for fast search purposes to reuse once calculated subtrees. Furthermore, trivial operations such as multiplying by one or zero, or adding or subtracting zero are eliminated to minimize the number of calculations during model evaluation.

|
A further advantage of using this internal representation is the
possibility to solve the general problem of permutations of some
operators (e.g. distributive law) in a very fast manner without
searching for equality of permutative terms. The simple but effective
mechanism of key calculation of a hash table offers the possibility to
get rid of the severe problem of permutations. Consider a simple
example where ![]() variables are to be added
variables are to be added
![]() . This
results in
. This
results in ![]() possible trees to represent this problem. To search an
already existing tree would need an enormous amount of time and
therefore a different mechanism must be found to optimize the tree.
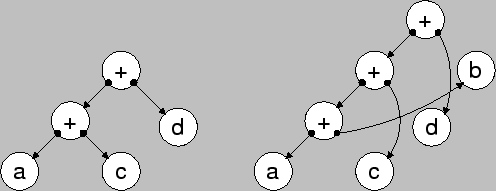
The best approach to get rid of this problem is simply avoiding the
search mechanism by using a specific way of tree assembling, which
guarantees a definite combination of the resulting tree. In other
words, no matter in which order the N variables are given the
resulting tree must always be the same. This condition can be
satisfied by calculating a hash key of a node and depending on the
result a recursive reorganization of the tree has to be done
(Fig. 6).
possible trees to represent this problem. To search an
already existing tree would need an enormous amount of time and
therefore a different mechanism must be found to optimize the tree.
The best approach to get rid of this problem is simply avoiding the
search mechanism by using a specific way of tree assembling, which
guarantees a definite combination of the resulting tree. In other
words, no matter in which order the N variables are given the
resulting tree must always be the same. This condition can be
satisfied by calculating a hash key of a node and depending on the
result a recursive reorganization of the tree has to be done
(Fig. 6).
|