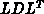 Vorkonditionierer
Vorkonditionierer




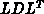 Vorkonditionierer
Vorkonditionierer
Eine unvollständige 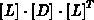 Zerlegung von
Zerlegung von  kann als effizienter Vorkonditionierer für symmetrische
Matrizen verwendet werden [van89].
Man versteht darunter eine partielle Cholesky-Zerlegung,
bei der jedes Auffüllen von Nebendiagonalelementen unterdrückt wird. Im Zusammenhang
mit CG-Lösern gehört die Methode zur Klasse der ICCG
(Incomplete Cholesky Conjugate Gradient)-Löser. Da kein Auffüllen der Nebendiagonalelemente
erlaubt ist, spricht man von einem ICCG(0) Löser.
Eine vollständige symmetrische Faktorisierung einer Matrix
kann als effizienter Vorkonditionierer für symmetrische
Matrizen verwendet werden [van89].
Man versteht darunter eine partielle Cholesky-Zerlegung,
bei der jedes Auffüllen von Nebendiagonalelementen unterdrückt wird. Im Zusammenhang
mit CG-Lösern gehört die Methode zur Klasse der ICCG
(Incomplete Cholesky Conjugate Gradient)-Löser. Da kein Auffüllen der Nebendiagonalelemente
erlaubt ist, spricht man von einem ICCG(0) Löser.
Eine vollständige symmetrische Faktorisierung einer Matrix  kann immer nur dann erfolgen,
wenn die Matrix
kann immer nur dann erfolgen,
wenn die Matrix  symmetrisch, positiv definit und eine M-Matrix ist.
Die genannten Vorbedingungen gelten ebenso für eine unvollständige Zerlegung von
symmetrisch, positiv definit und eine M-Matrix ist.
Die genannten Vorbedingungen gelten ebenso für eine unvollständige Zerlegung von  [van89][Mei77][Man79].
[van89][Mei77][Man79].
Die Vorkonditionierungsmatrix wird aus 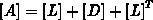 in der
heuristischen Form
in der
heuristischen Form
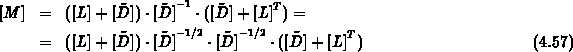
angesetzt.
Unter der Forderung, daß die Matrix  möglichst genau approximiert wird, wobei nur die
Diagonalmatrix
möglichst genau approximiert wird, wobei nur die
Diagonalmatrix 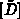 variiert und
variiert und 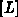 bzw.
bzw. 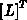 unverändert bleiben,
ergibt sich folgende Rechnung:
unverändert bleiben,
ergibt sich folgende Rechnung:
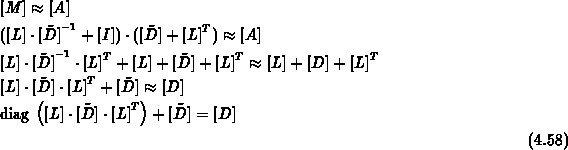
Die Rekursion
welche die unvollständige Cholesky-Faktorisierung beschreibt, ist in Komponentenschreibweise ohne Berücksichtigung komprimierter Matrixformate z.B. als
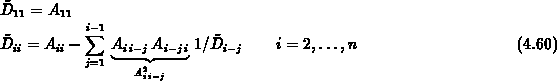
anzuschreiben.
Es ist natürlich effizienter, gleich 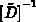 zu berechnen
und dazu die Rekursion mit
zu berechnen
und dazu die Rekursion mit 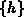 in die Form
in die Form
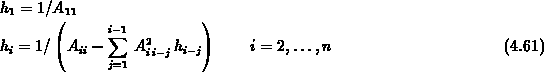
zu bringen.
Als Ergebnis erhält man die invertierte Diagonalmatrix 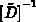 , die im
Vektor
, die im
Vektor 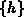 zurückgegeben wird.
zurückgegeben wird.
Das zu lösende System 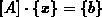 wird zunächst in seiner
vorkonditionierten Form
wird zunächst in seiner
vorkonditionierten Form

angeschrieben. Für die weitere Rechnung ist es vorteilhaft,  mit
mit 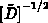 symmetrisch
symmetrisch
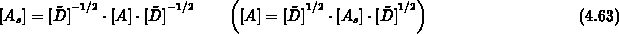
zu skalieren.
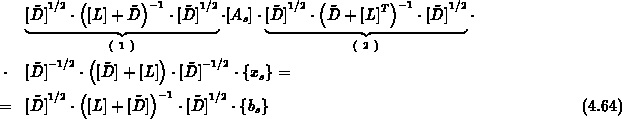
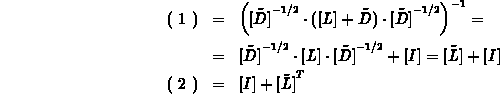
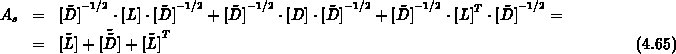
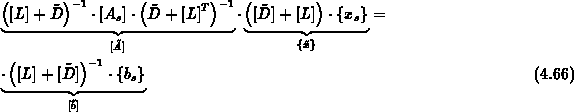
Der vorkonditionierte CG-Löser kann daher auf der neuen Struktur
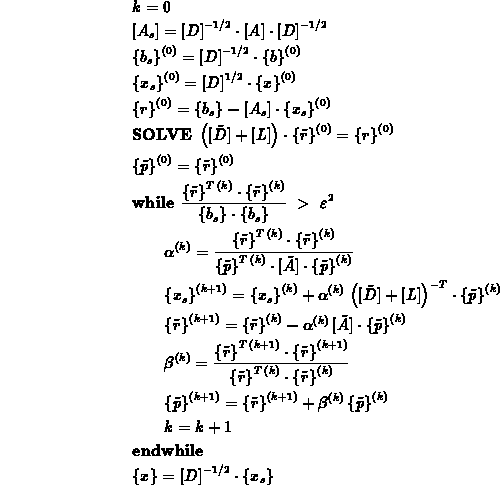
operieren.
In Abschnitt 4.5.4 wird erwähnt, daß es nicht notwendig ist, den Ausdruck
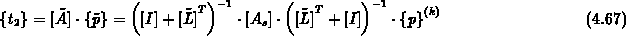
direkt zu bilden, sondern durch eine Matrix-Vektor-Multiplikation, eine Rücksubstitution und eine Vorwärtselimination
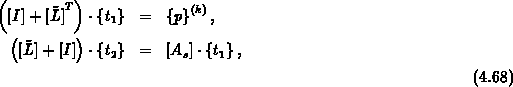
zu ersetzen. In [Eis81] wird gezeigt, daß sich der Aufwand stark reduziert, wenn folgende Identitäten ausgenützt werden:
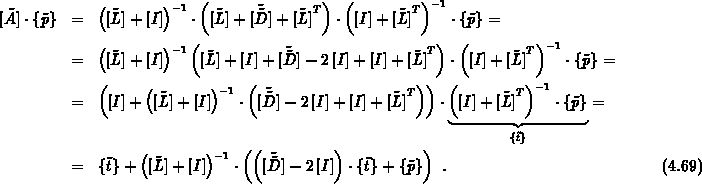
Bei dieser als Eisenstat-Trick bekannten Methode wird die
Multiplikation 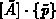 durch eine Vorwärtselimination,
eine Vektormultiplikation und eine Rücksubstitution in der Art
durch eine Vorwärtselimination,
eine Vektormultiplikation und eine Rücksubstitution in der Art
ersetzt.
Die Vorwärtselimination (4.71) kann auch für die Berechnung von
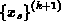 herangezogen werden.
Eine unwesentliche, aber einfach zu implementierende Verbesserung des Algorithmus erhält man dadurch, daß
man nicht
herangezogen werden.
Eine unwesentliche, aber einfach zu implementierende Verbesserung des Algorithmus erhält man dadurch, daß
man nicht 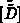 , sondern
, sondern 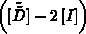 abspeichert.
Es ist auch anzumerken, daß man während der Iteration mit
abspeichert.
Es ist auch anzumerken, daß man während der Iteration mit

arbeiten kann und nach der Iteration die Lösung
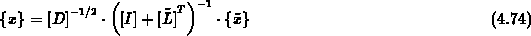
rückskaliert und rücksubstituiert.



