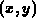 -Koordinatensystem auf ein
Einheitsquadrat im
-Koordinatensystem auf ein
Einheitsquadrat im 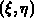 Koordinatensystem abgebildet werden
(Abbildungen 5.15 und 5.16),
und die Koordinatenlinien (Isolinien für konstantes
Koordinatensystem abgebildet werden
(Abbildungen 5.15 und 5.16),
und die Koordinatenlinien (Isolinien für konstantes 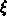 oder
oder 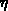 ) des
Einheitsquadrats sollen ebenfalls auf
) des
Einheitsquadrats sollen ebenfalls auf 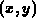 transformiert werden.
transformiert werden.




Anschaulich läßt sich die Methode in zwei Dimensionen erklären. Es soll ein
viereckiges Gebiet mit krummlinigen Kanten im 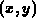 -Koordinatensystem auf ein
Einheitsquadrat im
-Koordinatensystem auf ein
Einheitsquadrat im 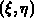 Koordinatensystem abgebildet werden
(Abbildungen 5.15 und 5.16),
und die Koordinatenlinien (Isolinien für konstantes
Koordinatensystem abgebildet werden
(Abbildungen 5.15 und 5.16),
und die Koordinatenlinien (Isolinien für konstantes 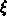 oder
oder 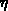 ) des
Einheitsquadrats sollen ebenfalls auf
) des
Einheitsquadrats sollen ebenfalls auf 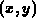 transformiert werden.
transformiert werden.
Das besondere Merkmal dieser Methode ist, daß der Rand des Einheitsquadrats
exakt auf den Rand im 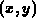 Koordinatensystem transformiert wird.
Koordinatensystem transformiert wird.
Die Anwendung der beiden unabhängigen Projektoren auf 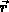 ergibt mit
ergibt mit
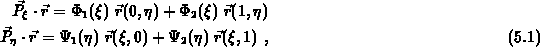
jeweils eine unidirektionale Interpolation in 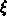 - oder
- oder 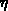 -Richtung.
-Richtung.
Der Produktprojektor
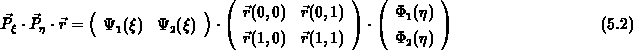
interpoliert von den vier Eckpunkten ausgehend in zwei Richtungen und entspricht der Tensorproduktform.
Der Boolsche Summenprojektor 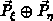 interpoliert
von der gesamten Berandung ausgehend in zwei Richtungen
interpoliert
von der gesamten Berandung ausgehend in zwei Richtungen
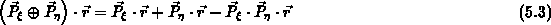
und in der vereinfachten Form

wobei 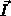 den Einsvektor darstellt.
den Einsvektor darstellt.
Diese Operatoren können auch in drei Dimensionen die gewünschte transfinite Interpolation nach einem ähnlichen Schema mit
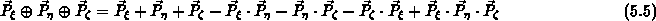
aufbauen. Die vereinfachte Form ergibt sich zu
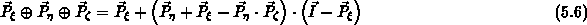
und in der optimierteren Form
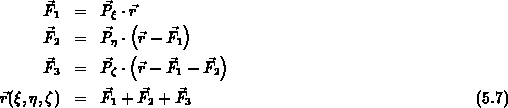
mit
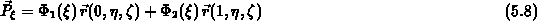
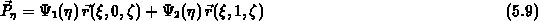
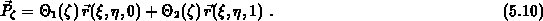
Soll ein hexaederförmiges Hyper-Element zerlegt werden, so sind zunächst die sechs
Randflächen mit zweidimensionaler transfiniter Interpolation 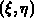 ,
aber mit räumlichen Koordinaten
,
aber mit räumlichen Koordinaten 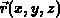 , in Vierecke zu zerlegen,
und dann ist mit transfiniter Interpolation und dem kurvenlinearen Koordinatensystem
, in Vierecke zu zerlegen,
und dann ist mit transfiniter Interpolation und dem kurvenlinearen Koordinatensystem
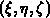 die räumliche Zerlegung, von den zerlegten Randflächen
ausgehend, in Hexaeder vorzunehmen.
die räumliche Zerlegung, von den zerlegten Randflächen
ausgehend, in Hexaeder vorzunehmen.