2.2.8 Die Momentenmethode




Next: 2.3 Klassische Thermodynamik (Thermostatik)
Up: 2.2 Statistische Mechanik
Previous: 2.2.7 Formale Transporttheorie
Der lokale, gewichtete Mittelwert der Momentenfunktion
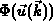 im
Geschwindigkeitsraum wird als Moment bezeichnet [180].
Unter der Voraussetzung der Existenz einer konstanten, skalaren effektiven
Masse, die ihrerseits eine isotrope, parabolische Bandstruktur voraussetzt,
ist die Geschwindigkeit dem Kristallimpuls proportional (2.35).
Die Momentenbildung im
im
Geschwindigkeitsraum wird als Moment bezeichnet [180].
Unter der Voraussetzung der Existenz einer konstanten, skalaren effektiven
Masse, die ihrerseits eine isotrope, parabolische Bandstruktur voraussetzt,
ist die Geschwindigkeit dem Kristallimpuls proportional (2.35).
Die Momentenbildung im 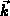 -Raum erfolgt mit Hilfe von Gl. (2.31)
gemäß
-Raum erfolgt mit Hilfe von Gl. (2.31)
gemäß

und liefert einen Wert für 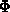 am Ort
am Ort 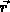 zur Zeit
zur Zeit 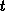 .
Der Nenner in Gl. (2.100) ist der Elektronenkonzentration proportional.
.
Der Nenner in Gl. (2.100) ist der Elektronenkonzentration proportional.
Die Momentenmethode stellt ein formales Verfahren dar, um aus der
Boltzmann Transportgleichung Bilanzgleichungen für makroskopische
Größen abzuleiten.
Zu diesem Zweck wird die Boltzmanngleichung
mit einer beliebigen, geschwindigkeitsabhängigen Größe 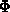 multipliziert und anschließend über alle Geschwindigkeiten (bzw. im
multipliziert und anschließend über alle Geschwindigkeiten (bzw. im
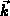 -Raum) integriert.
Auf diese Weise kann die Boltzmanngleichung, die im allgemeinen Fall
eine partielle Integro-Differentialgleichung im Phasenraum
darstellt, in eine Serie von
-Raum) integriert.
Auf diese Weise kann die Boltzmanngleichung, die im allgemeinen Fall
eine partielle Integro-Differentialgleichung im Phasenraum
darstellt, in eine Serie von  gekoppelten, partiellen
Differentialgleichungen im Ortsraum entwickelt werden, die allerdings
gekoppelten, partiellen
Differentialgleichungen im Ortsraum entwickelt werden, die allerdings
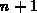 Unbekannte enthält.
Um ein geschlossenes Gleichungssystem zu erhalten, muß die
Momentenentwicklung abgebrochen und geeignete zusätzliche Annahmen gemacht
werden.
Im Hinblick auf die Bestimmung der Verteilungsfunktion bedeutet deswegen
jedes durch die Momentenentwicklung der Boltzmanngleichung
hergeleitete hydrodynamische Transportmodell
einen Informationsverlust gegenüber der Boltzmanngleichung.
Unbekannte enthält.
Um ein geschlossenes Gleichungssystem zu erhalten, muß die
Momentenentwicklung abgebrochen und geeignete zusätzliche Annahmen gemacht
werden.
Im Hinblick auf die Bestimmung der Verteilungsfunktion bedeutet deswegen
jedes durch die Momentenentwicklung der Boltzmanngleichung
hergeleitete hydrodynamische Transportmodell
einen Informationsverlust gegenüber der Boltzmanngleichung.
Das hydrodynamische Transportmodell umfaßt die ersten drei oder vier
Momente der Boltzmanngleichung.
Das nullte Moment liefert eine Kontinuitätsgleichung für die
Ladungsträgerkonzentration.
Die mittlere Teilchengeschwindigkeit tritt als Unbekannte auf.
Das erste Moment liefert eine Kontinuitätsgleichung
für den mittleren Impuls der Ladungsträger.
Die mittlere kinetische Energie pro Ladungsträger tritt als Unbekannte auf.
Das zweite Moment liefert eine Kontinuitätsgleichung für die
kinetische Energiedichte, in der allerdings der Wärmefluß unbestimmt
bleibt.
Das erste Moment entspricht der Eulergleichung der Hydrodynamik.
Entwickelt man den Drucktensor erhält man die Navier-Stokes Gleichung.
Das zweite Moment entspricht dem Energiesatz der Hydrodynamik.
Multipliziert man die Boltzmanngleichung (2.74) mit
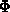 und summiert über alle Zustände im
und summiert über alle Zustände im 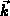 -Raum ergibt sich
[120], [178]:
-Raum ergibt sich
[120], [178]:
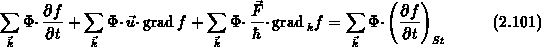
Mit Hilfe der Produktregel und unter Berücksichtigung der
Unabhängigkeit
der Momentenfunktion 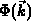 von Ort und Zeit ergibt sich aus
Gl. (2.101):
von Ort und Zeit ergibt sich aus
Gl. (2.101):
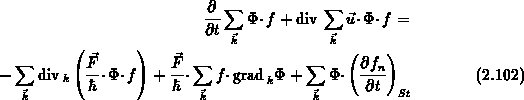
Der erste Term der rechten Seite verschwindet, weil 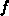 mit
mit 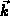 schnell null wird (Gaußscher Integralsatz).
Berücksichtigt man
die Definition der Ladungsträgerdichte erhält man
folgende allgemeine Transportgleichung für verschiedene Momente von
schnell null wird (Gaußscher Integralsatz).
Berücksichtigt man
die Definition der Ladungsträgerdichte erhält man
folgende allgemeine Transportgleichung für verschiedene Momente von
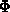 [120], [180]:
[120], [180]:
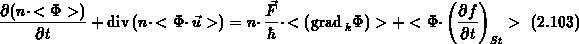
Gl. (2.103) hat die Form einer Kontinuitätsgleichung.
Der zweite Term enthält den korrespondierenden Fluß.
Die rechte Seite besteht aus einem Generationsterm, der den Einfluß
der äußeren Kraft beschreibt, und einen Rekombinationsterm,
der die Wirkung der Streuprozesse enthält.
Das nullte Moment der Boltzmanngleichung folgt unmittelbar aus
Gl. (2.103) für 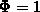 :
:
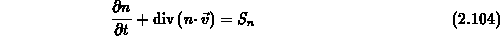
Gl. (2.104) enthält die mittlere Geschwindigkeit 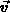 als
Unbekannte.
Das Produkt
als
Unbekannte.
Das Produkt 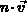 stellt die Teilchenstromdichte dar.
stellt die Teilchenstromdichte dar.
Das erste Moment der Boltzmanngleichung ergibt sich aus Gl. (2.103),
wenn man nacheinander für 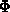 die Komponenten
die Komponenten 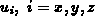 einsetzt und
anschließend alle drei
Komponentenkontinuitätsgleichungen zusammenfaßt
(
einsetzt und
anschließend alle drei
Komponentenkontinuitätsgleichungen zusammenfaßt
(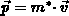 ):
):
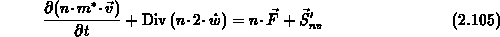
Der erste Term der rechten Seite beschreibt die Impulsgeneration aufgrund
der Beschleunigung der Ladungsträger in Richtung der äußeren Kraft.
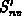 bedeutet den Impulsverlust durch Streuprozesse.
Um den Tensor der mittleren kinetischen Energie pro Ladungsträger
bedeutet den Impulsverlust durch Streuprozesse.
Um den Tensor der mittleren kinetischen Energie pro Ladungsträger 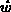 zu entwickeln, werden lokale Relativgeschwindigkeiten definiert
[120], [160], [178], [180]:
zu entwickeln, werden lokale Relativgeschwindigkeiten definiert
[120], [160], [178], [180]:

Die Gruppengeschwindigkeit 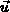 läßt sich als Summe zweier Anteile
darstellen.
läßt sich als Summe zweier Anteile
darstellen.
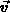 ist die Driftgeschwindigkeit der Elektronen unter dem Einfluß
äußerer Kräfte.
ist die Driftgeschwindigkeit der Elektronen unter dem Einfluß
äußerer Kräfte.
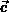 bezeichnet die zufällige Geschwindigkeit des
Ladungsträgers aufgrund der thermischen Anregung.
Der größte Anteil der Teilchenbewegung ist zufällig und durch die
thermische Energie des Teilchens bedingt. Mit Gl. (2.106) ergibt sich
(
bezeichnet die zufällige Geschwindigkeit des
Ladungsträgers aufgrund der thermischen Anregung.
Der größte Anteil der Teilchenbewegung ist zufällig und durch die
thermische Energie des Teilchens bedingt. Mit Gl. (2.106) ergibt sich
(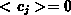 ) [120]:
) [120]:
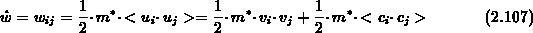
Gewöhnlich wird der letzte Summand in Gl. (2.107) zur Definition
eines Temperaturtensors verwendet [120], [160], [178],
[180]:
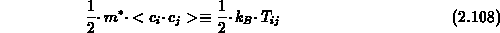
Gl. (2.108) stellt die kinetische Definition der Temperatur dar.
Es ist zu beachten, daß der in Gl. (2.107) und (2.108)
hergestellte Zusammenhang von
Bandenergie und Temperatur eine parabolische Bandstruktur impliziert.
Setzt man Gl. (2.107) und (2.108) in Gl. (2.105)
ein, erhält man nach der Division mit 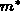 :
:
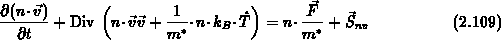
Der Ausdruck 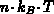 kann entsprechend der Zustandsgleichung
des idealen Gases als Druck des Elektronengases betrachtet werden.
kann entsprechend der Zustandsgleichung
des idealen Gases als Druck des Elektronengases betrachtet werden.
Setzt man 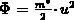 in die allgemeine
Transportgleichung (2.103) ein, ergibt sich das zweite Moment der
Boltzmanngleichung:
in die allgemeine
Transportgleichung (2.103) ein, ergibt sich das zweite Moment der
Boltzmanngleichung:
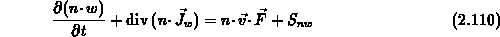
Die mittlere kinetische Energie pro Ladungsträger  folgt aus
Gl. (2.107) und (2.108):
folgt aus
Gl. (2.107) und (2.108):
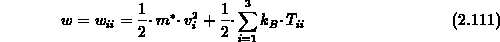
Der erste Summand stellt die Feldenergie dar, der zweite die thermische
Energie.
Die kinetische Energie aus dem Feld erscheint kurz nach dem Anlegen
hoher, externer Felder als Drift-Energie.
Die Streuung produziert eine
große, zufällige Komponente der Geschwindigkeit,
sodaß die kinetische
Energie aus dem Feld schließlich als thermische Energie auftritt
[120].
Die Energieflußdichte unter dem Divergenzoperator in
Gl. (2.110) kann mit Hilfe von Gl. (2.106)
folgendermaßen
entwickelt werden [120], [160]:
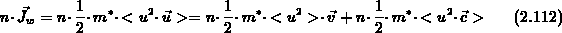
Daraus ergibt sich (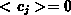 ):
):
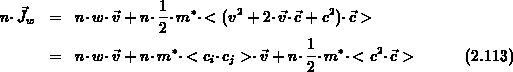
Der letzte Summand kann als Wärmefluß interpretiert
werden [120], [160]:
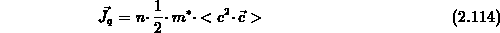
Mit der Definition des Temperaturtensors (2.108)
und des Wärmeflusses (2.114) folgt
aus Gl. (2.110) und Gl. (2.113):
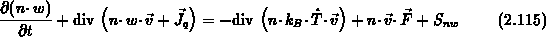
Die Flußdichte der kinetischen Energie besteht aus drei Anteilen.
Der erste Term bezeichnet die 'kinetische Energiedichte' eines
Volumenelementes mal der
Geschwindigkeit, mit der sich dieses Volumen bewegt.
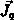 beschreibt den Energieverlust dieses Volumenelementes durch
Wärmeleitung.
Der erste Term der rechten Seite stellt die
Arbeit dar, um ein Volumenelement gegen den Druck des Elektronengases
mit
beschreibt den Energieverlust dieses Volumenelementes durch
Wärmeleitung.
Der erste Term der rechten Seite stellt die
Arbeit dar, um ein Volumenelement gegen den Druck des Elektronengases
mit 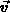 zu bewegen.
Der zweite Ausdruck bezeichnet eine
Quelle kinetischer Energie aufgrund einer äußeren Kraft.
zu bewegen.
Der zweite Ausdruck bezeichnet eine
Quelle kinetischer Energie aufgrund einer äußeren Kraft.
Gl. (2.104), (2.109) und (2.115) stellen drei Gleichungen
für die Unbekannten  ,
, 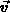 ,
,  und
und 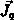 dar.
Sowohl die Impulsbilanzgleichung (2.109) wie die
Bilanzgleichung der kinetischen Energie (2.115) haben die
Normalform der kontinuumsmechanischen Hydrodynamik.
Der korrespondierende Fluß setzt sich
jeweils aus einem Konvektions- und einem Leitungsanteil zusammen
[115], [180].
Gl. (2.109), (2.115)
können vereinfacht werden, wenn der Temperaturtensor
näherungsweise als Skalar aufgefaßt wird (
dar.
Sowohl die Impulsbilanzgleichung (2.109) wie die
Bilanzgleichung der kinetischen Energie (2.115) haben die
Normalform der kontinuumsmechanischen Hydrodynamik.
Der korrespondierende Fluß setzt sich
jeweils aus einem Konvektions- und einem Leitungsanteil zusammen
[115], [180].
Gl. (2.109), (2.115)
können vereinfacht werden, wenn der Temperaturtensor
näherungsweise als Skalar aufgefaßt wird (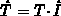 ).
Diese Vereinfachung impliziert die Annahme, daß die thermische Energie
auch im Nichtgleichgewicht gleichmäßig auf die Freiheitsgrade
verteilt ist wie im Gleichgewicht.
Unter dieser Voraussetzung vereinfacht sich Gl. (2.111):
).
Diese Vereinfachung impliziert die Annahme, daß die thermische Energie
auch im Nichtgleichgewicht gleichmäßig auf die Freiheitsgrade
verteilt ist wie im Gleichgewicht.
Unter dieser Voraussetzung vereinfacht sich Gl. (2.111):
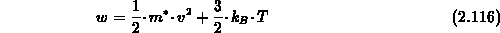
Um das System hydrodynamischer Gleichungen abzuschließen wird
der Wärmefluß 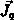 mit Hilfe der phänomenologischen
Gleichung von Fourier [101], [115], [151] auf die skalare
Temperatur zurückgeführt:
mit Hilfe der phänomenologischen
Gleichung von Fourier [101], [115], [151] auf die skalare
Temperatur zurückgeführt:

Mit 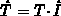 und Gl. (2.117) ergibt sich:
und Gl. (2.117) ergibt sich:
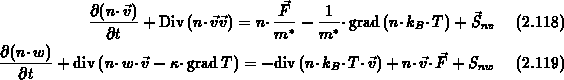
Durch Subtraktion der mit 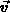 bzw.
bzw.  gewichteten
Ladungsträgerkontinuitätsgleichung (2.104)
kann
Gl. (2.118) bzw. (2.119) weiter vereinfacht werden:
gewichteten
Ladungsträgerkontinuitätsgleichung (2.104)
kann
Gl. (2.118) bzw. (2.119) weiter vereinfacht werden:
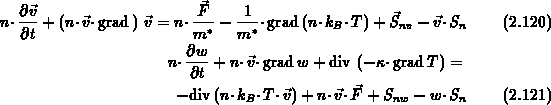
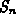 ,
, 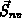 und
und 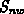 bezeichnen die zeitliche Änderung
von
bezeichnen die zeitliche Änderung
von  ,
, 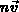 und
und  aufgrund von Streuprozessen.
Übergänge infolge von Streuprozessen umfassen Interband- und
Intrabandübergänge, wobei letztere ihrerseits in Intertal- und
Intratalübergänge unterteilt werden.
Nur Übergänge zwischen Bändern können die Teilchenkonzentration
verändern.
In diesem Sinn kann
aufgrund von Streuprozessen.
Übergänge infolge von Streuprozessen umfassen Interband- und
Intrabandübergänge, wobei letztere ihrerseits in Intertal- und
Intratalübergänge unterteilt werden.
Nur Übergänge zwischen Bändern können die Teilchenkonzentration
verändern.
In diesem Sinn kann 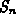 als die Rate der Interbandübergänge
interpretiert und zur Definition einer Nettorekombinationsrate
als die Rate der Interbandübergänge
interpretiert und zur Definition einer Nettorekombinationsrate 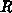 verwendet
werden.
Separiert man Interband- und Intrabandübergänge in
verwendet
werden.
Separiert man Interband- und Intrabandübergänge in
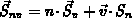 und
und 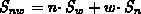 ,
können die Summen der beiden Streuterme der rechten Seiten von
Gl. (2.120), (2.121) als Nettoraten der zeitlichen
Änderung von
,
können die Summen der beiden Streuterme der rechten Seiten von
Gl. (2.120), (2.121) als Nettoraten der zeitlichen
Änderung von 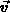 und
und  infolge von Intrabandübergängen
erkannt werden [17], [60], [160]:
infolge von Intrabandübergängen
erkannt werden [17], [60], [160]:
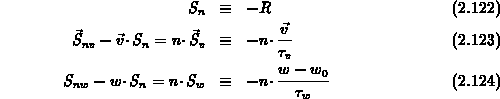
Gl. (2.122), (2.123), (2.124) sind Definitionen, keine
Approximationen.
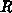 stellt die Nettorekombinationsrate der Ladungsträger dar.
Gewöhnlich werden Impuls- und
Energierelaxationszeiten definiert, weil
die direkte Bestimmung von
stellt die Nettorekombinationsrate der Ladungsträger dar.
Gewöhnlich werden Impuls- und
Energierelaxationszeiten definiert, weil
die direkte Bestimmung von 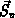 ,
, 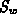 aus der allgemeinen
Transportgleichung
(2.103) die Kenntnis der (unbekannten)
Nichtgleichgewichtsverteilungsfunktion
aus der allgemeinen
Transportgleichung
(2.103) die Kenntnis der (unbekannten)
Nichtgleichgewichtsverteilungsfunktion 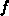 verlangt.
Allerdings erfordert auch die Bestimmung der Relaxationszeiten
entweder Monte Carlo Simulationen oder
Annahmen über die Form der Verteilungsfunktion [120].
verlangt.
Allerdings erfordert auch die Bestimmung der Relaxationszeiten
entweder Monte Carlo Simulationen oder
Annahmen über die Form der Verteilungsfunktion [120].
Um zu der in der Bauelementesimulation üblichen Form der Bilanzgleichungen
zu gelangen, müssen Gl. (2.104), (2.120), (2.121)
- unter Berücksichtigung der Definitionen (2.122), (2.123),
(2.124) -
mit Hilfe der elektrischen Stromdichte 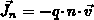 ,
der elektrischen Feldstärke
,
der elektrischen Feldstärke 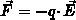 und
der Beweglichkeit
und
der Beweglichkeit 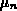

umgeformt werden (zusätzlich werden die Größen  ,
,  und
und
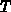 mit dem Index
mit dem Index  dem Elektronensystem zugeordnet).
Das hydrodynamische Transportmodell für Elektronen hat folgende Gestalt
[60], [160]:
dem Elektronensystem zugeordnet).
Das hydrodynamische Transportmodell für Elektronen hat folgende Gestalt
[60], [160]:
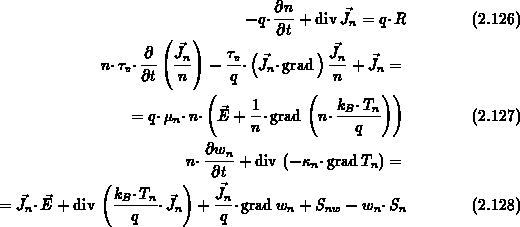
Durch weitere Vereinfachungen erhält man aus Gl. (2.126),
(2.127) und (2.128) das seit den
Anfängen der Bauelementesimulation verwendete
Drift-Diffusionsmodell.
Es wird eine einheitliche, homogene Temperatur für Ladungsträger und
das Kristallgitter angenommen.
Somit kann die Energiebilanzgleichung
als Bestimmungsgleichung für die Elektronentemperatur vernachlässigt
werden.
In der Impulsbilanzgleichung können wegen der Kleinheit der
Impulsrelaxationszeit 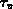 die ersten zwei Terme weggelassen
werden [160].
Der zweite Term der linken Seite in Gl. (2.127)
stellt den Impulsstrom aufgrund der Driftgeschwindigkeit dar.
Er wird oft
gegenüber dem Impulstransport aufgrund thermischer Anregung schon im
Ansatz (2.109) nicht mehr berücksichtigt [168].
Die Vernachlässigung des konvektiven Anteils des Impulsstromes
entspricht der Vernachlässigung der Driftkomponente der kinetischen
Energiedichte in Gl. (2.107).
die ersten zwei Terme weggelassen
werden [160].
Der zweite Term der linken Seite in Gl. (2.127)
stellt den Impulsstrom aufgrund der Driftgeschwindigkeit dar.
Er wird oft
gegenüber dem Impulstransport aufgrund thermischer Anregung schon im
Ansatz (2.109) nicht mehr berücksichtigt [168].
Die Vernachlässigung des konvektiven Anteils des Impulsstromes
entspricht der Vernachlässigung der Driftkomponente der kinetischen
Energiedichte in Gl. (2.107).
Die stationäre Impulsbilanzgleichung stellt die Stromrelation des
Drift-Diffusionsmodells dar:
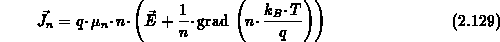
Benutzt man die Einsteinrelation zur Definition einer Diffusionskonstante,
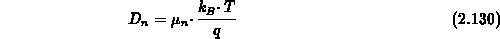
erhält man wegen der Ortsunabhängigkeit von 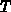 (Annahme konstanter Temperatur) die endgültige
Form der Stromrelation für das Drift-Diffusionsmodell:
(Annahme konstanter Temperatur) die endgültige
Form der Stromrelation für das Drift-Diffusionsmodell:
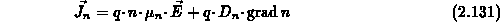
Gl. (2.129) wird als Näherung der
Impulsbilanzgleichung für das Drift-Diffusions-, für das
thermoelektrische sowie für das hydrodynamische Transportmodell verwendet.
Eine Voraussetzung der Momentenmethode ist die Gültigkeit des Konzepts
einer konstanten, skalaren effektiven Masse eines Ladungsträgers im
periodischen Kristallgitter.
Diese Bedingung setzt ihrerseits istrope, parabolische Bandstruktur
voraus.
Im nichtparabolischen Fall gibt es keinen einfachen analytischen Zusammenhang
des Wellenvektors 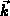 mit der Gruppengeschwindigkeit
mit der Gruppengeschwindigkeit 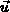 des Elektrons,
des mittleren Impulses
des Elektrons,
des mittleren Impulses 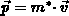 und der Driftgeschwindigkeit,
sowie der
kinetischen Energie
und der Driftgeschwindigkeit,
sowie der
kinetischen Energie  und der Temperatur
und der Temperatur 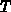 .
Gl. (2.35), (2.107), (2.108), (2.116)
sind nicht mehr gültig.
Tatsächlich müssen
.
Gl. (2.35), (2.107), (2.108), (2.116)
sind nicht mehr gültig.
Tatsächlich müssen 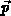 und
und 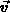 , sowie
, sowie
 und
und 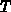 jeweils als zwei Variablen betrachtet werden.
Die Konsequenz
ist
die Ungültigkeit der in diesem Abschnitt hergeleiteten Impuls- und
Energiebilanzgleichung.
jeweils als zwei Variablen betrachtet werden.
Die Konsequenz
ist
die Ungültigkeit der in diesem Abschnitt hergeleiteten Impuls- und
Energiebilanzgleichung.




Next: 2.3 Klassische Thermodynamik (Thermostatik)
Up: 2.2 Statistische Mechanik
Previous: 2.2.7 Formale Transporttheorie
Martin Stiftinger
Sat Jun 10 15:00:12 MET DST 1995
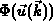 im
Geschwindigkeitsraum wird als Moment bezeichnet [180].
Unter der Voraussetzung der Existenz einer konstanten, skalaren effektiven
Masse, die ihrerseits eine isotrope, parabolische Bandstruktur voraussetzt,
ist die Geschwindigkeit dem Kristallimpuls proportional (2.35).
Die Momentenbildung im
im
Geschwindigkeitsraum wird als Moment bezeichnet [180].
Unter der Voraussetzung der Existenz einer konstanten, skalaren effektiven
Masse, die ihrerseits eine isotrope, parabolische Bandstruktur voraussetzt,
ist die Geschwindigkeit dem Kristallimpuls proportional (2.35).
Die Momentenbildung im 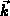 -Raum erfolgt mit Hilfe von Gl. (2.31)
gemäß
-Raum erfolgt mit Hilfe von Gl. (2.31)
gemäß





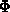 am Ort
am Ort 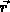 zur Zeit
zur Zeit 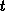 .
Der Nenner in Gl. (
.
Der Nenner in Gl. ( gekoppelten, partiellen
Differentialgleichungen im Ortsraum entwickelt werden, die allerdings
gekoppelten, partiellen
Differentialgleichungen im Ortsraum entwickelt werden, die allerdings
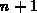 Unbekannte enthält.
Um ein geschlossenes Gleichungssystem zu erhalten, muß die
Momentenentwicklung abgebrochen und geeignete zusätzliche Annahmen gemacht
werden.
Im Hinblick auf die Bestimmung der Verteilungsfunktion bedeutet deswegen
jedes durch die Momentenentwicklung der Boltzmanngleichung
hergeleitete hydrodynamische Transportmodell
einen Informationsverlust gegenüber der Boltzmanngleichung.
Unbekannte enthält.
Um ein geschlossenes Gleichungssystem zu erhalten, muß die
Momentenentwicklung abgebrochen und geeignete zusätzliche Annahmen gemacht
werden.
Im Hinblick auf die Bestimmung der Verteilungsfunktion bedeutet deswegen
jedes durch die Momentenentwicklung der Boltzmanngleichung
hergeleitete hydrodynamische Transportmodell
einen Informationsverlust gegenüber der Boltzmanngleichung.
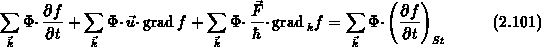
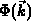 von Ort und Zeit ergibt sich aus
Gl. (
von Ort und Zeit ergibt sich aus
Gl. (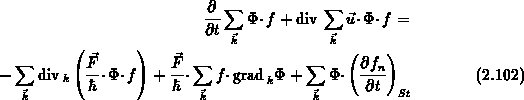
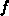 mit
mit 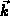 schnell null wird (Gaußscher Integralsatz).
Berücksichtigt man
die Definition der Ladungsträgerdichte erhält man
folgende allgemeine Transportgleichung für verschiedene Momente von
schnell null wird (Gaußscher Integralsatz).
Berücksichtigt man
die Definition der Ladungsträgerdichte erhält man
folgende allgemeine Transportgleichung für verschiedene Momente von
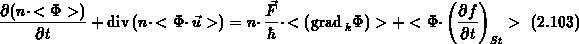
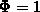 :
:
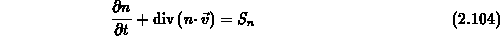
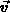 als
Unbekannte.
Das Produkt
als
Unbekannte.
Das Produkt 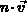 stellt die Teilchenstromdichte dar.
stellt die Teilchenstromdichte dar.
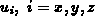 einsetzt und
anschließend alle drei
Komponentenkontinuitätsgleichungen zusammenfaßt
(
einsetzt und
anschließend alle drei
Komponentenkontinuitätsgleichungen zusammenfaßt
(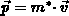 ):
):
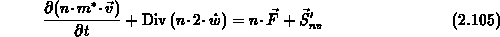
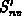 bedeutet den Impulsverlust durch Streuprozesse.
Um den Tensor der mittleren kinetischen Energie pro Ladungsträger
bedeutet den Impulsverlust durch Streuprozesse.
Um den Tensor der mittleren kinetischen Energie pro Ladungsträger 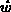 zu entwickeln, werden lokale Relativgeschwindigkeiten definiert
zu entwickeln, werden lokale Relativgeschwindigkeiten definiert

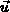 läßt sich als Summe zweier Anteile
darstellen.
läßt sich als Summe zweier Anteile
darstellen.
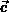 bezeichnet die zufällige Geschwindigkeit des
Ladungsträgers aufgrund der thermischen Anregung.
Der größte Anteil der Teilchenbewegung ist zufällig und durch die
thermische Energie des Teilchens bedingt. Mit Gl. (
bezeichnet die zufällige Geschwindigkeit des
Ladungsträgers aufgrund der thermischen Anregung.
Der größte Anteil der Teilchenbewegung ist zufällig und durch die
thermische Energie des Teilchens bedingt. Mit Gl. (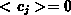 )
) 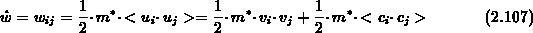
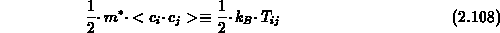
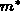 :
:
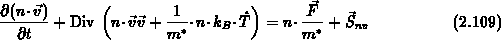
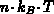 kann entsprechend der Zustandsgleichung
des idealen Gases als Druck des Elektronengases betrachtet werden.
kann entsprechend der Zustandsgleichung
des idealen Gases als Druck des Elektronengases betrachtet werden.
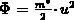 in die allgemeine
Transportgleichung (
in die allgemeine
Transportgleichung (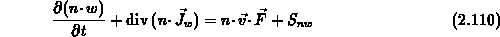
 folgt aus
Gl. (
folgt aus
Gl. (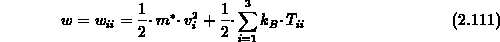
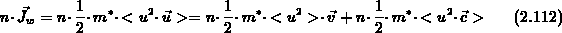
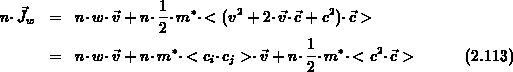
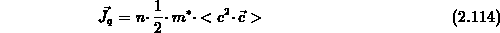
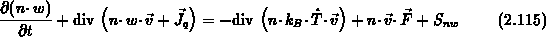
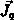 beschreibt den Energieverlust dieses Volumenelementes durch
Wärmeleitung.
Der erste Term der rechten Seite stellt die
Arbeit dar, um ein Volumenelement gegen den Druck des Elektronengases
mit
beschreibt den Energieverlust dieses Volumenelementes durch
Wärmeleitung.
Der erste Term der rechten Seite stellt die
Arbeit dar, um ein Volumenelement gegen den Druck des Elektronengases
mit 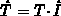 ).
Diese Vereinfachung impliziert die Annahme, daß die thermische Energie
auch im Nichtgleichgewicht gleichmäßig auf die Freiheitsgrade
verteilt ist wie im Gleichgewicht.
Unter dieser Voraussetzung vereinfacht sich Gl. (
).
Diese Vereinfachung impliziert die Annahme, daß die thermische Energie
auch im Nichtgleichgewicht gleichmäßig auf die Freiheitsgrade
verteilt ist wie im Gleichgewicht.
Unter dieser Voraussetzung vereinfacht sich Gl. (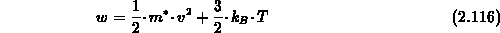

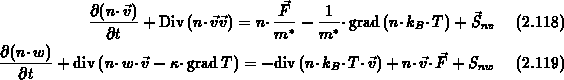
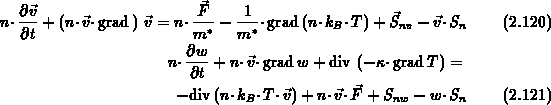
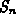 ,
, 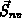 und
und 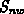 bezeichnen die zeitliche Änderung
von
bezeichnen die zeitliche Änderung
von 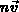 und
und  aufgrund von Streuprozessen.
Übergänge infolge von Streuprozessen umfassen Interband- und
Intrabandübergänge, wobei letztere ihrerseits in Intertal- und
Intratalübergänge unterteilt werden.
Nur Übergänge zwischen Bändern können die Teilchenkonzentration
verändern.
In diesem Sinn kann
aufgrund von Streuprozessen.
Übergänge infolge von Streuprozessen umfassen Interband- und
Intrabandübergänge, wobei letztere ihrerseits in Intertal- und
Intratalübergänge unterteilt werden.
Nur Übergänge zwischen Bändern können die Teilchenkonzentration
verändern.
In diesem Sinn kann 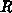 verwendet
werden.
Separiert man Interband- und Intrabandübergänge in
verwendet
werden.
Separiert man Interband- und Intrabandübergänge in
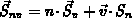 und
und 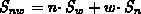 ,
können die Summen der beiden Streuterme der rechten Seiten von
Gl. (
,
können die Summen der beiden Streuterme der rechten Seiten von
Gl. (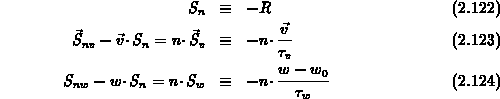
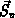 ,
, 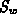 aus der allgemeinen
Transportgleichung
(
aus der allgemeinen
Transportgleichung
(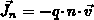 ,
der elektrischen Feldstärke
,
der elektrischen Feldstärke 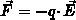 und
der Beweglichkeit
und
der Beweglichkeit 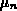

 und
und
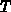 mit dem Index
mit dem Index 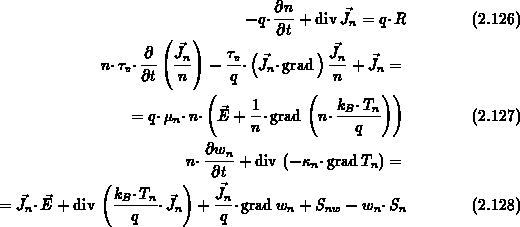
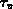 die ersten zwei Terme weggelassen
werden
die ersten zwei Terme weggelassen
werden 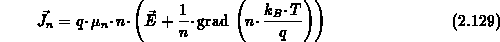
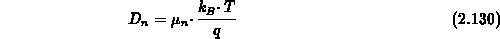
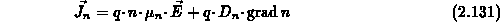
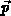 und
und