Next: 2.8 General Solving Procedure Up: 2. Finite Element Method Previous: 2.6 Newton Methods

2.7 Assembling

For a problem described by a system of PDEs a local matrix for each element of the discretization $T_h(\Omega)$ , nucleus, is constructed. This nucleus is integrated into the general matrix of the system through a process called assembling. In this section the assembling algorithm applied in numerical schemes of problems discussed in Chapters 3 and 4 is derived.

The Jacobi matrix needed for the Newton method in the case of a finite element discretization is,

$\displaystyle \mathbf{G}=\frac{\partial (\ell_{1,1},\dots,\ell_{1,N},\dots,\ell... ...ots,\ell_{M,N})}{\partial (c_{1,1},\dots,c_{1,N},\dots,c_{M,1},\dots,c_{M,N})}.$

(2.40)

In the further text we will call this Jacobi matrix general matrix. The inputs of the general matrix are calculated according to,

$\displaystyle g(p+N(q-1),a+N(b-1))=\frac{\partial\ell_{qp}(c_{1,1},\dots,c_{1,N},\dots,c_{M,1},\dots,c_{M,N})}{\partial c_{ab}},$

(2.41)

where $p,a\in\{1,\dots,N\}$ , $q,b\in\{1,\dots,M\}$ , and the discrete operators $\ell_{qp}$ are calculated as integrals over the discretization $T_h(\Omega)$ .
The calculation of the general matrix $\mathbf{G}$ by the inner product $(\varphi_i,\mathcal{L}(\mathbf{c}_h))_{h}$ over the whole discretisized domain $T_h(\Omega)$ is rarely utilized in computer programs. A common approach is to construct the matrix $\mathbf{G}$ by assembling it out of the nucleus matrix $\Pi_T$ which is calculated for each element $T\in T_h(\Omega)$ [11],

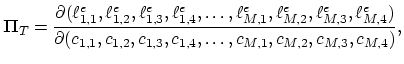$\displaystyle \mathbf{\Pi}_T=\frac{\partial (\ell_{1,1}^e,\ell_{1,2}^e,\ell_{1,... ...rtial (c_{1,1},c_{1,2},c_{1,3},c_{1,4},\dots,c_{M,1},c_{M,2},c_{M,3},c_{M,4})},$

(2.42)

with the inputs,

$\displaystyle \mathbf{\pi}_T(s+4(p-1),r+4(l-1))=\frac{\partial\ell_{sp}^e(c_{1,1},\dots,c_{1,N},\dots,c_{M,1},\dots,c_{M,N})}{\partial c_{rl}},$

(2.43)

where $s,r\in\{1,2,3,4\}$ and $p,l\in\{1,\dots,M\}$ .

The basic nodal function $\varphi_A$ , defined at the arbitrary point $A\in T_h(\Omega)$ is non-zero only on the patch . Furthermore $\varphi_A$ can be represented as,

$\displaystyle \varphi_A = \sum_{T\in P(A)} \varphi_A^T.$

(2.44)

$\varphi_A^T=1$ at the point and $\varphi_A^T=0$ at three other points of the tethraedal element .

The discrete operators $\ell_{ap}$ obtained by testing of -th equation of the system with the basic nodal function $\varphi_A$ is,

$\displaystyle \ell_{ap}=(\varphi_A,\mathcal{L}_p(\mathbf{c}_h))_{T_h(\Omega)}=\sum_{T\in P(A)}(\varphi_A^T,\mathcal{L}_p(\mathbf{c}_h))_{T}.$

(2.45)

The partial derivative of (2.45) with respect to $c_{kl}$ is,

$\displaystyle \frac{\partial \ell_{ap}}{\partial c_{kl}}=\sum_{T\in P(A)}\frac{... ... c_{1,i} \varphi_i,\dots,\sum_{i=1}^4 c_{M,i}\varphi_i))_{T}}{\partial c_{kl}}.$

(2.46)

Obviously in (2.46) $\varphi_A^T$ is equal to one of the basic nodal functions $\varphi_1,\varphi_2,\varphi_3,\varphi_4$ at the element . Furthermore, the partial derivative is non-zero only if the $c_{kl}$ stays for one nodal value of .

We now define the operator $\chi(T,i)$ , $T\in T_h(\Omega)$ , , which assigns a single global index to every local index of vertex belonging to the tethraedal element . The inverse function $\chi^{-1}(T,I)$ is also well-defined.

From (2.41), (2.43), and (2.46) we have,

$\displaystyle g(a+N(p-1),k+N(l-1))=\frac{\partial \ell_{ap}}{\partial c_{kl}}=\sum_{T\in P(A)}\mathbf{\pi}_T(\chi^{-1}(T,a)+4(p-1),\chi^{-1}(T,k)+4(l-1)).$

(2.47)

The assembling process consists of calculating of nucleus matrix $\mathbf{\Pi}_T$ for each element of the mesh $T_h(\Omega)$ and building the inputs of the global matrix $\mathbf{G}$ as the sum on the right side of the equation (2.47). For the implementation of the assembling algorithm into software tools the following algorithm is used,

At the end of the assembling process the general matrix $\mathbf{G}$ contains the values given by (2.40).

Next: 2.8 General Solving Procedure Up: 2. Finite Element Method Previous: 2.6 Newton Methods

H. Ceric: Numerical Techniques in Modern TCAD