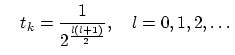


Next: 2.7 Assembling
Up: 2. Finite Element Method
Previous: 2.5 Finite Element Spaces
Subsections
2.6 Newton Methods
The discretization of the non-linear PDE systems leads to a large system of nonlinear algebraic
equations. There are various methods which solve such systems. Among them the most popular is a Newton method with it's variations.
Generally we have a system of N non-linear algebraic equations
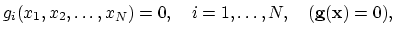 |
(2.32) |
assuming that the functions 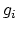 have continues first order derivations with respect to
have continues first order derivations with respect to 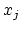 .
If the values
.
If the values 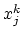
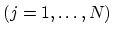 of the
of the 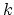 -th approximate solution are known, we write Taylor series expansion of the functions
-th approximate solution are known, we write Taylor series expansion of the functions 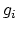 in the vicinity of
in the vicinity of 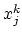 ,
,
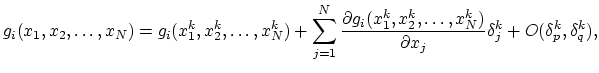 |
(2.33) |
for
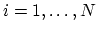 , where
, where
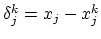 .
By choosing for
.
By choosing for 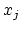 the exact value
the exact value 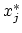 and neglecting the terms of order
and neglecting the terms of order
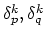 we have from (2.33)
we have from (2.33)
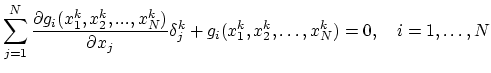 |
(2.34) |
The matrix
![$\displaystyle [\mathbf{J}]_{N\times N},\quad J_{ij}=\frac{\partial f_i(x_1^{k}, x_2^{k},\dots,x_{N}^{k})}{\partial x_j},$](img134.png) |
(2.35) |
is called Jacobi matrix. In the case when this matrix is non-singular the linear equation system (2.34) can be solved. Depending on the problem itself different types of linear solvers should be applied [11].
The solutions of the linear system (2.34) are the increments
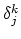
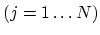 and with these increments we can calculate new approximation,
and with these increments we can calculate new approximation,
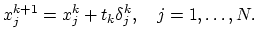 |
(2.36) |
The determination of damping value 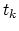 is the question of trial and error. The sequences often used for subsequent trials are,
is the question of trial and error. The sequences often used for subsequent trials are,
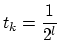 or or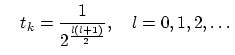 |
(2.37) |
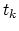 is accepted if the following criterion is fulfilled,
is accepted if the following criterion is fulfilled,
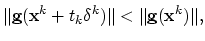 |
(2.38) |
where we use Euclidian norm.
Since the calculation of the Jacobi matrix is a very computer resources-consuming procedure, one can for a number of subsequent Newton iterations also use the same Jacobi matrix (2.35). In that case on obtains,
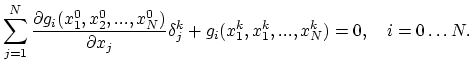 |
(2.39) |
The simplified Newton method obviously has a worse convergence behavior.
2.6.4 Damping
In the cases where the convergence of the Newton scheme is attainable only for a very small time steps, methods for the enforcing of the convergence must be applied.
The method which has also successfully been applied in semiconductor device modelling [4], is the so-called Bank-Rose algorithm [12].
Figure 2.3:
Bank-Rose algorithm.
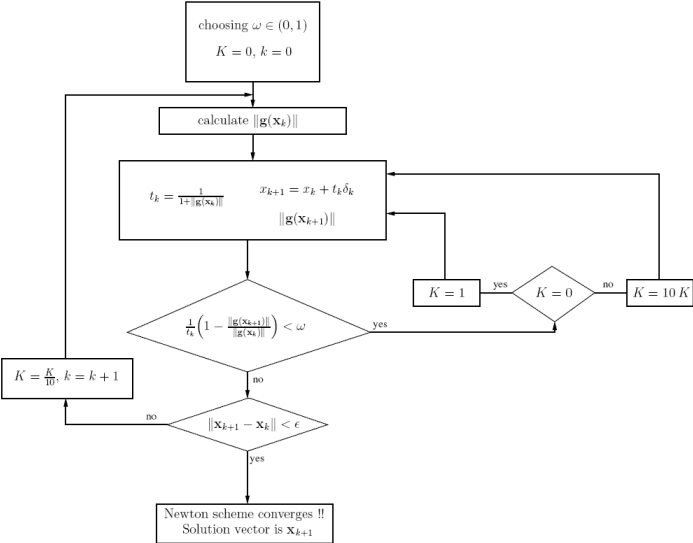
|
The algorithm is represented in Figure 2.3. It controls the behavior of Newton scheme through a damping factor 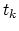 .
The parameter of crucial importance for the algorithm is
.
The parameter of crucial importance for the algorithm is 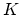 . In Figure 2.3 we take
. In Figure 2.3 we take 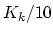 as initial estimate for
as initial estimate for 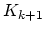 . Alternatively, we have used
. Alternatively, we have used
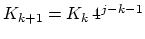 , where
, where 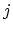 is the counter of failed tests
is the counter of failed tests
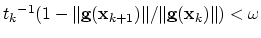 .
.
The algorithm searchs through the vincinity of the initial solution
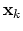 for the shortest path through the attraction region of the Newton scheme to reach the next approximation
for the shortest path through the attraction region of the Newton scheme to reach the next approximation
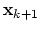 . In the cases when the Bank-Rose algorithm fails the parameter
. In the cases when the Bank-Rose algorithm fails the parameter 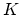 grows infinitely and an improved approximation
grows infinitely and an improved approximation
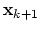 is never found.
is never found.



Next: 2.7 Assembling
Up: 2. Finite Element Method
Previous: 2.5 Finite Element Spaces
H. Ceric: Numerical Techniques in Modern TCAD
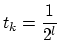 or
or