Next: 2 The Diffuse Interface
Up: 5 Void evolution and
Previous: 5 Void evolution and
We assumed unpassivated monocrystal isotropic interconnects where
stress phenomena can be neglected.
An interconnect is idealized as two-dimensional electrically
conducting via which contains initially a circular void. For simplicity we also neglect the effects of grain boundaries and lattice diffusion.
In this case there are two main forces which influence the shape of
the evolving void interface: the chemical potential gradient and
electron wind.
The first force causes self-diffusion of metal atoms on
the void interface and tends to minimize energy which results in
circular void shapes.
The electron wind force produces asymmetry in
the void shape depending on the electrical field gradients.
Including contributions from both, electromigration and chemical
potential-driven surface diffusion, gives the total surface atomic
flux,
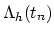 =
=
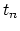 , where
, where 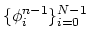 is the unit vector
tangent to the void surface [60,87]
is the unit vector
tangent to the void surface [60,87]
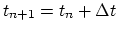 |
(253) |
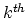 is the effective valence (Section 4.2),
is the effective valence (Section 4.2), 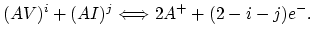 is the charge of an
electron,
is the charge of an
electron,
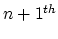 is the local component of the
electric field tangential to the void surface,
is the local component of the
electric field tangential to the void surface, 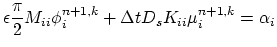 is the local
surface curvature, and
is the local
surface curvature, and 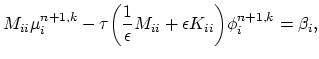 is the surface gradient operator;
is the surface gradient operator;
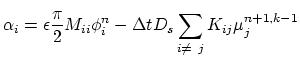 , where
, where 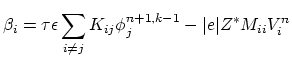 is the local unit vector
normal to the void surface.
Further,
is the local unit vector
normal to the void surface.
Further,
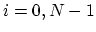 is the
surface energy,
is the
surface energy, 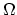 is the volume of an atom, and
is the volume of an atom, and 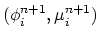 is given
through an Arrhenius law:
is given
through an Arrhenius law:
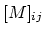 exp exp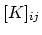 |
(254) |
Here, 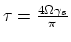 is the thickness of the diffusion layer,
is the thickness of the diffusion layer, 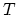 is the temperature,
is the temperature, 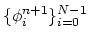 is the
activation energy for the surface diffusion, and
is the
activation energy for the surface diffusion, and 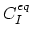 is the
pre-exponential factor for mass diffusion.
Equation (4.43) is the Nernst-Einstein equation, where the sum in
the parentheses on the right side expresses the driving force.
Mass conservation gives the void propagation velocity normal to the
void surface,
is the
pre-exponential factor for mass diffusion.
Equation (4.43) is the Nernst-Einstein equation, where the sum in
the parentheses on the right side expresses the driving force.
Mass conservation gives the void propagation velocity normal to the
void surface, 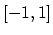 , through the continuity equation [61,63,87],
, through the continuity equation [61,63,87],
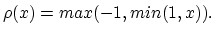 |
(255) |
The electric field 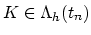 can be written as the gradient of the
electric potential, i.e.,
can be written as the gradient of the
electric potential, i.e.,
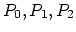 |
(256) |
The field is also solenoidal, i.e.,
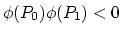 |
(257) |
Equations (4.46) and (4.47) imply that the potential 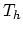 obeys Laplace's equation,
obeys Laplace's equation,
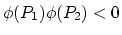 |
(258) |
The void surface and the interconnects edges are modeled as
insulating boundaries, i.e.
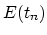 |
(259) |
at these boundaries.




Next: 2 The Diffuse Interface
Up: 5 Void evolution and
Previous: 5 Void evolution and
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
![]() =
=
![]() , where
, where ![]() is the unit vector
tangent to the void surface [60,87]
is the unit vector
tangent to the void surface [60,87]
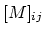 exp
exp