7 Grid Adaptation

The grid adaption algorithm used in this work is a version of the algorithm introduced in [89] and consists of a grid refinement algorithm and a grid coarsening algorithm. The refinement algorithm is based on recursive bisecting of triangles. A triangle is marked for refinement if it complies with some specific refinement criterion 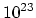$COND$. In our application we used 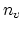$COND=IGRC$ for the initial refinement and 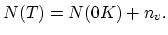$COND=TGRC$ for the grid maintaining refinement. For every triangle of the grid, the longest one of its edges is marked as refinement edge. The element and its neighbor element which also contains the same refinement edge are refined by bisecting this edge (Fig. 4.6). We can define refinement of the element in the following way:

Now, the overall refinement algorithm can be formulated as follows:

The parameter max_refinement_depth limits the number of bisecting of a triangle. The grid is refined until there is no more element marked for refinement or the maximal refinement depth is reached.
The coarsening algorithm is more or less the inverse of the refinement algorithm. Each element that does not fullfil criterion 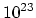$COND$ is marked for coarsening. The basic idea is to find the father element whose refinement produced the element in consideration.

The following routine coarsens as many elements as possible, even more than once if allowed:

The complete adaption of the grid is reached by sequential invoking of the grid refinement and of the grid coarsening algorithm.