3.2 Elektrische Größen eines n-Pols

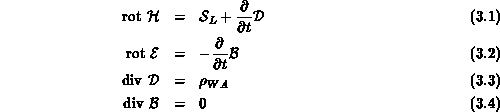
  Die Maxwell'schen Gleichungen für das elektromagnetische Feld lauten [83]:

Für den stationären Fall gelten die folgenden vereinfachten Beziehungen:

In den Gleichungen 3.1 bis 3.6 kommen die folgenden physikalischen Größen vor:

Aus diesen Grundgrößen werden die elektrischen Integralgrößen Strom (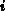), Spannung (), Ladung (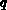) und Fluß (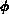), welche Funktionen der Zeit 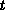und der Temperatur 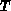sein können, abgeleitet:

Die Größen 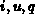und 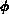reichen aus, um einen allgemeinen idealen n-Pol (Abbildung 3.1) unter den in Abschnitt 3.1 angegebenen Vereinfachungen vollständig zu beschreiben.

  
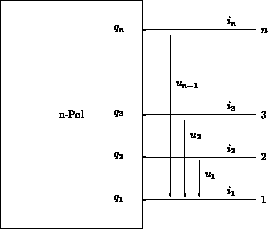
Abbildung 3.1: Allgemeiner n-Pol

Die meisten Netzwerkanalyseprogramme finden jedoch nur mit den Größen 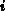und das Auslangen. Die Hinzunahme der Größen 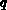und 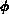zur Beschreibung eines Bauteils wird von [29][20] unterstützt. In [20] wird anhand von Beispielschaltungen gezeigt, daß die Anzahl der notwendigen Iterationen bei der Simulation auf ein Drittel reduziert werden kann. Chua schlägt in [29] 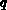und 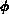als die beste Wahl für die Zustandsgrößen des Differentialgleichungssystems aus elektrischer und numerischer Sicht vor.

Die beschreibenden Größen eines n-Pols sind nun:

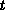, Zeit [s]

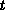  ist der Zeitpunkt, zu dem der Zustand des n-Pols betrachtet wird.

, Spannung [V]

  Einer der Anschlüsse eines Bauteils wird als Bezugsanschluß ausgewählt. Für den n-Pol wird ein Zählpfeilsystem derart definiert, daß alle Zählpfeile für den n-Pol zum Bezugsanschluß zeigen. Die Zählpfeile entsprechen also dem Fall, daß alle Spannungen positiv sind und daher der Bezugsanschluß ein negativeres Potential als alle anderen Anschlüsse hat. Der Vektor ist der Vektor der Potentialdifferenzen der übrigen Anschlüsse gegenüber dem Bezugsanschluß. Der Vektor besteht aus Elementen.

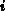, Strom [A]

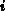  Ein Strom, der in den n-Pol hinein fließt, wird positiv gerechnet. ist ein Vektor bestehend aus den Strömen in den Anschlüssen. Wie in Abschnitt 3.3 gezeigt werden wird, sind diese Ströme nicht voneinander unabhängig, vielmehr hat man im allgemeinsten Fall nur unabhängige Ströme.

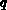, Speicherladung [C]

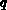      Der Vektor gibt die Größe der gespeicherten (wahren) Ladungen an, die sich auf den, den entsprechenden Anschlüssen zugeordneten, Elektroden eines n-Pols befinden. Das Vorzeichen der Ladung ist positiv, wenn die wahre Ladung auf der Elektrode positiv ist.

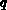kann auch als ``elektrisches Gedächtnis'' des Bauteils aufgefaßt werden. Analog zum Stromvektor besteht der Ladungsvektor aus maximal unabhängigen Werten (siehe 3.3). Das elektrische Feld des idealen Bauteils befindet sich nur innerhalb des Bauteils. Das Bauteil muß daher elektrisch abgeschirmt sein, es befindet sich in einem Faraday'schen Käfig.

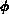, magnetischer Fluß [Wb]

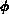  Der Vektor besteht aus den Elementen der verketteten Flüsse des n-Pols. Das gesamte magnetische Feld des idealisierten n-Pols befindet sich nur innerhalb des Bauteils. Das Bauteil ist magnetisch abgeschirmt gedacht. Analog zum Ladungsvektor 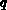beschreibt der Vektor 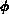die in Form des magnetischen Feldes gespeicherte Energie, also das ``magnetische Gedächtnis''.

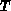, Temperatur [K]

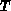  ist die absolute Temperatur, die das gesamte Bauteil hat. Da das Bauteil gemäß den Annahmen in Abschnitt 3.1 infinitesimal klein ist, ist die Temperatur in jedem Punkt des Bauteils gleich.

Wenn man sich nicht für eine Analyse der Temperaturverteilung im Netzwerk interessiert, kann die Temperatur 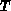als Parameter der Bauelementeigenschaften behandelt werden.

Die Zeit 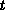, zu der der n-Pol betrachtet wird, ist für die mathematische Betrachtung ein von außen eingeprägter Parameter.

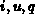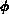Die Eigenschaften und spannen somit einen Parameterraum, den idealen Netzwerkraum, auf.