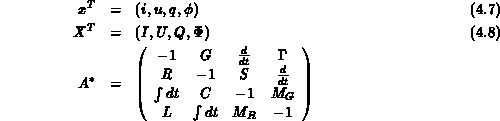4.1 Beschreibung linearer dynamischer Zweipole




Next: 4.2 Charakteristische Eigenschaften eines
Up: 4 Elektrische lineare Zweipole
Previous: 4 Elektrische lineare Zweipole
Durch die Reduzierung der Anschlüsse des Bauteils auf zwei, ergeben sich
folgende Vereinfachungen:
-
Der Spannungsvektor besteht nur aus einem einzigen Element, der
Potentialdifferenz zwischen den beiden Anschlüssen.
Der Bezugsanschluß wird bei Zweipolen als ``negativer'' Anschluß,
der andere als ``positiver'' Anschluß bezeichnet.
Dadurch wird eine Zählpfeilrichtung für die Spannung definiert.
- Der Stromvektor besteht aus zwei entgegengesetzt gleichen Elementen.
Es reicht daher vollkommen aus, nur einen Strom für den Zweipol anzugeben.
Es muß jedoch eine Zählpfeilrichtung für Ströme eingeführt werden.
Der Strom, der in den ``positiven'' Anschluß hinein fließt wird positiv
genommen.
Durch diese Zählpfeilrichtung, die mit der Zählpfeilrichtung
der Spannung übereinstimmt, haben die entsprechenden Bauteileigenschaften
(R, L, C, etc.) einen positiven Wert.
Üblicherweise wird daher eine derartige Zählpfeilrichtung für
Ströme und Spannungen gewählt.
- Wie der Stromvektor besteht der Ladungsvektor aus zwei
entgegengesetzt gleichen Werten.
Es reicht daher auch hier die Angabe eines Wertes aus,
wobei folgende Zählpfeilrichtung definiert wird.
Die Ladungen, die sich auf der Elektrode befinden, die dem ``positiven''
Anschluß zugeordnet ist, wird positiv gezählt
und repräsentiert gleichzeitig den negativen Wert der Ladung auf der
anderen Elektrode.
- Der Flußvektor besteht analog zum Spannungsvektor aus nur einem Element.
Die Zählpfeilrichtung ist so gewählt, daß die positive Flußrichtung
vom ``positiven'' zum ``negativen'' Anschluß gerichtet ist.
- Die Zählpfeilrichtungen für
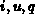 und
und 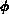 sind so gewählt,
daß für passive Bauteile die gespeicherte Energie und die elektrisch
verbrauchte Leistung
als positives Produkt der entsprechenden Größen ermittelt werden kann.
Dieses Zählpfeilsystem wird Verbraucherzählpfeilsystem
genannt, da es bei Bauteilen, die elektrische Energie in eine andere
Energieform (Wärme, Kraft, etc.) umwandeln, zu positiven
Energiewerten führt.
sind so gewählt,
daß für passive Bauteile die gespeicherte Energie und die elektrisch
verbrauchte Leistung
als positives Produkt der entsprechenden Größen ermittelt werden kann.
Dieses Zählpfeilsystem wird Verbraucherzählpfeilsystem
genannt, da es bei Bauteilen, die elektrische Energie in eine andere
Energieform (Wärme, Kraft, etc.) umwandeln, zu positiven
Energiewerten führt.
Durch die oben angeführten Vereinfachungen kann ein Zweipol nun mit
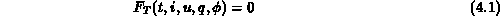
beschrieben werden. Es treten keine Vektoren mehr auf.
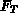 stellt die charakteristische Funktionenmenge für die Temperatur T
des Bauelements dar.
stellt die charakteristische Funktionenmenge für die Temperatur T
des Bauelements dar.
Ein Bauteil ist linear, wenn 4.1 ein
Gleichungssystem mit linearen Operatoren (algebraisch oder
differentiell) ist. Der Rang des Gleichungssystems kann maximal 4 sein.
Das volle Gleichungssystem hat somit folgendes Aussehen:
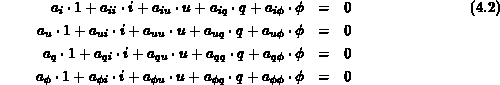
Die Faktoren 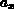 stellen die Quellen dar.
Die
stellen die Quellen dar.
Die 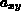 können bei einem linearen dynamischen Bauteil folgende
lineare Operatoren
und deren Verknüpfungen durch Addition, Subtraktion oder Multiplikation sein:
können bei einem linearen dynamischen Bauteil folgende
lineare Operatoren
und deren Verknüpfungen durch Addition, Subtraktion oder Multiplikation sein:

Je nach den verknüpften  und
und 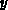 haben die
haben die 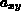 entsprechende
Dimensionen.
entsprechende
Dimensionen.
In Matrixschreibweise hat das Gleichungssystem 4.2
folgendes Aussehen (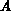 ist eine Operatormatrix):
ist eine Operatormatrix):
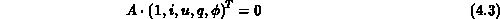
Falls das Gleichungssystem 4.3 keine Lösung besitzt,
so existiert dieser Zweipol nicht.
Es sind daher nicht sämtliche Kombinationen von 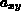 für existierende
Zweipole erlaubt.
Kriterien für die Existenz sind z.B. in [30][29] zu finden.
für existierende
Zweipole erlaubt.
Kriterien für die Existenz sind z.B. in [30][29] zu finden.
Die Existenz eines Operators 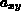 bedeutet,
daß die Größe
bedeutet,
daß die Größe  durch die Größe
durch die Größe 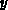 gesteuert wird.
Z.B. bedeutet
gesteuert wird.
Z.B. bedeutet 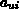 , daß mittels des Operators
, daß mittels des Operators 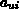 , dem ohmschen
Widerstand, eine Spannung in Abhängigkeit vom Strom
, dem ohmschen
Widerstand, eine Spannung in Abhängigkeit vom Strom 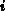 eingeprägt wird.
Dies bedeutet jedoch in der Regel nicht, daß mittels des
Operators
eingeprägt wird.
Dies bedeutet jedoch in der Regel nicht, daß mittels des
Operators 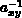 die Größe
die Größe 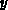 durch
durch  gesteuert wird, da nicht
gefordert ist, daß der inverse Operator zu
gesteuert wird, da nicht
gefordert ist, daß der inverse Operator zu 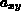 existiert
(z.B. ist
existiert
(z.B. ist 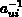 für
für 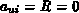 nicht definiert).
nicht definiert).
In der Gleichung
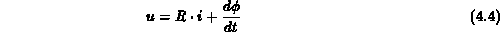
bedeutet 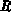 die Steuerung eines Teils der Spannung
die Steuerung eines Teils der Spannung  durch den Strom
durch den Strom 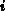 .
Ein Rückschluß von
.
Ein Rückschluß von  auf
auf 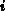 ist in trivialer Weise nicht möglich.
ist in trivialer Weise nicht möglich.
Falls eine Zeile des Gleichungssystems 4.3 ``existiert'',
muß zumindestens das Element 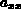 ungleich dem 0-Operator
und ungleich 0 für alle möglichen Fälle sein.
Der Operator
ungleich dem 0-Operator
und ungleich 0 für alle möglichen Fälle sein.
Der Operator 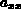 stellt eine gemeinsame Skalierung der Abhängigkeit der
Größe
stellt eine gemeinsame Skalierung der Abhängigkeit der
Größe  von den anderen Größen dar.
Ohne Skalierung ist
von den anderen Größen dar.
Ohne Skalierung ist 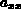 der Operator
der Operator 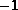 .
Im folgenden werden ohne Einschränkung der Allgemeinheit
für
.
Im folgenden werden ohne Einschränkung der Allgemeinheit
für 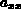 immer nur die Operatoren
immer nur die Operatoren 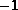 und
und  verwendet.
verwendet.
Ist der Rang der Matrix 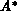 (siehe Gleichung 4.6) gleich
der Anzahl der
(siehe Gleichung 4.6) gleich
der Anzahl der  , für die es mindestens ein
, für die es mindestens ein 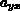 ungleich dem 0-Operator gibt,
so ist dieses Bauteil von außen nicht beeinflußbar,
es stellt eine Quelle dar.
In diesem Fall ist es auch möglich, daß das Gleichungssystem 4.3
überhaupt keine Lösung hat, das Bauteil also nicht existiert.
Die Matrix
ungleich dem 0-Operator gibt,
so ist dieses Bauteil von außen nicht beeinflußbar,
es stellt eine Quelle dar.
In diesem Fall ist es auch möglich, daß das Gleichungssystem 4.3
überhaupt keine Lösung hat, das Bauteil also nicht existiert.
Die Matrix 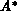 darf keine voneinander linear abhängigen Zeilen
besitzen.
darf keine voneinander linear abhängigen Zeilen
besitzen.
Die in einem elektrischen Grundbauteil auftretenden konkreten Operatoren
für die 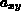 sind in Tabelle 4.1 zusammengefaßt
(die Bezeichnungen stammen aus den ISO-Normen 31 und 1000, die Symbole
sind in Tabelle 4.1 zusammengefaßt
(die Bezeichnungen stammen aus den ISO-Normen 31 und 1000, die Symbole
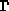 und
und 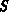 sind dem ANSI/IEEE Standard 280 entnommen [62]).
sind dem ANSI/IEEE Standard 280 entnommen [62]).
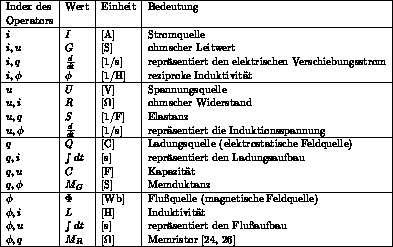
Abbildung 4.1: Operatoren zur Beschreibung eines Bauteils
Die Operatormatrix 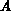 hat daher maximal folgendes Aussehen:
hat daher maximal folgendes Aussehen:
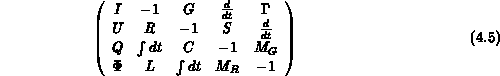
Eine physikalische Realisierung eines Bauteils mit einer vollen Matrix
ist nicht vorstellbar.
Für die meisten verwendeten idealen Bauteile sind fast alle
Elemente der Matrix 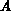 gleich dem 0-Operator.
gleich dem 0-Operator.
Die Operatormatrix 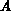 kann in Form eines bewerteten gerichteten
Graphen [44][28] dargestellt werden.
kann in Form eines bewerteten gerichteten
Graphen [44][28] dargestellt werden.
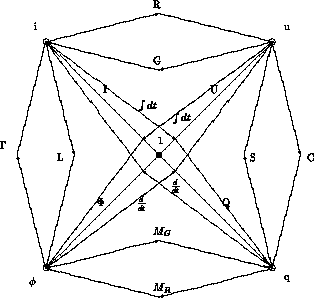
Abbildung 4.2: Charakteristischer Graph eines Bauelements
Abbildung 4.2 zeigt eine solche Darstellung für eine volle Matrix.
Die Knoten des Graphen sind die physikalischen Größen, die den
Zustand des Bauteils beschreiben.
Die Kanten des Graphen geben die Abhängigkeit einer Größe von einer
anderen an,
der Wert der Kante gibt die Art und Größe der Abhängigkeit an.
Eine Kante 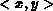 von der Größe
von der Größe  zur Größe
zur Größe 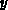 existiert genau dann,
wenn der Operator
existiert genau dann,
wenn der Operator 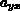 ungleich dem 0-Operator ist.
Die Operatoren
ungleich dem 0-Operator ist.
Die Operatoren 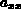 (Schleifen
(Schleifen 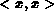 für den Knoten x) sind
nicht eingezeichnet.
für den Knoten x) sind
nicht eingezeichnet.
Enthält eine Zeile der Matrix 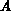 (4.5)
mehr als ein Element
(4.5)
mehr als ein Element 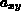 (
(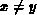 ) ungleich
) ungleich  ,
kann dies als Parallelschaltung bei den
,
kann dies als Parallelschaltung bei den 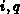 -Zeilen
oder als Serienschaltung bei den
-Zeilen
oder als Serienschaltung bei den 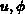 Zeilen
von 1 bis maximal 4 Grundeigenschaften aufgefaßt werden.
Zeilen
von 1 bis maximal 4 Grundeigenschaften aufgefaßt werden.
Durch Interpretation der Einheitsquellen als Inhomogenitäten
der Matrix 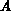 (4.5) gelangt man zu dem inhomogenen Gleichungssystem
(4.5) gelangt man zu dem inhomogenen Gleichungssystem

mit
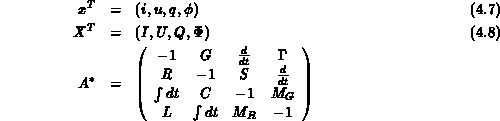




Next: 4.2 Charakteristische Eigenschaften eines
Up: 4 Elektrische lineare Zweipole
Previous: 4 Elektrische lineare Zweipole
Martin Stiftinger
Fri Jun 9 19:49:39 MET DST 1995
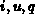 und
und 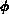 sind so gewählt,
daß für passive Bauteile die gespeicherte Energie und die elektrisch
verbrauchte Leistung
als positives Produkt der entsprechenden Größen ermittelt werden kann.
Dieses Zählpfeilsystem wird Verbraucherzählpfeilsystem
genannt, da es bei Bauteilen, die elektrische Energie in eine andere
Energieform (Wärme, Kraft, etc.) umwandeln, zu positiven
Energiewerten führt.
sind so gewählt,
daß für passive Bauteile die gespeicherte Energie und die elektrisch
verbrauchte Leistung
als positives Produkt der entsprechenden Größen ermittelt werden kann.
Dieses Zählpfeilsystem wird Verbraucherzählpfeilsystem
genannt, da es bei Bauteilen, die elektrische Energie in eine andere
Energieform (Wärme, Kraft, etc.) umwandeln, zu positiven
Energiewerten führt.




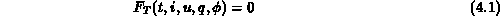
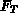 stellt die charakteristische Funktionenmenge für die Temperatur T
des Bauelements dar.
stellt die charakteristische Funktionenmenge für die Temperatur T
des Bauelements dar.
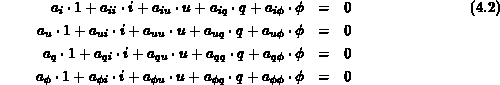
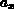 stellen die Quellen dar.
Die
stellen die Quellen dar.
Die 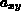 können bei einem linearen dynamischen Bauteil folgende
lineare Operatoren
und deren Verknüpfungen durch Addition, Subtraktion oder Multiplikation sein:
können bei einem linearen dynamischen Bauteil folgende
lineare Operatoren
und deren Verknüpfungen durch Addition, Subtraktion oder Multiplikation sein:

 und
und 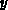 haben die
haben die 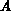 ist eine Operatormatrix):
ist eine Operatormatrix):
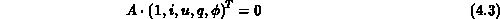
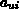 , daß mittels des Operators
, daß mittels des Operators 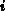 eingeprägt wird.
Dies bedeutet jedoch in der Regel nicht, daß mittels des
Operators
eingeprägt wird.
Dies bedeutet jedoch in der Regel nicht, daß mittels des
Operators 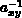 die Größe
die Größe 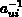 für
für 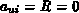 nicht definiert).
nicht definiert).
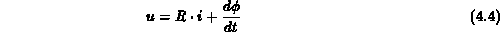
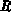 die Steuerung eines Teils der Spannung
die Steuerung eines Teils der Spannung  durch den Strom
durch den Strom 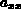 ungleich dem 0-Operator
und ungleich 0 für alle möglichen Fälle sein.
Der Operator
ungleich dem 0-Operator
und ungleich 0 für alle möglichen Fälle sein.
Der Operator 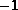 .
Im folgenden werden ohne Einschränkung der Allgemeinheit
für
.
Im folgenden werden ohne Einschränkung der Allgemeinheit
für  verwendet.
verwendet.
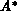 (siehe Gleichung
(siehe Gleichung 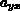 ungleich dem 0-Operator gibt,
so ist dieses Bauteil von außen nicht beeinflußbar,
es stellt eine Quelle dar.
In diesem Fall ist es auch möglich, daß das Gleichungssystem
ungleich dem 0-Operator gibt,
so ist dieses Bauteil von außen nicht beeinflußbar,
es stellt eine Quelle dar.
In diesem Fall ist es auch möglich, daß das Gleichungssystem 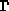 und
und 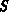 sind dem ANSI/IEEE Standard 280 entnommen
sind dem ANSI/IEEE Standard 280 entnommen 
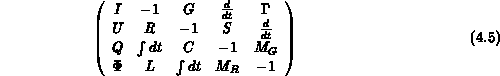

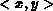 von der Größe
von der Größe 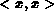 für den Knoten x) sind
nicht eingezeichnet.
für den Knoten x) sind
nicht eingezeichnet.
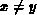 ) ungleich
) ungleich 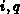 -Zeilen
oder als Serienschaltung bei den
-Zeilen
oder als Serienschaltung bei den 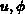 Zeilen
von 1 bis maximal 4 Grundeigenschaften aufgefaßt werden.
Zeilen
von 1 bis maximal 4 Grundeigenschaften aufgefaßt werden.