Discretization of momentum space

2.3 Discretization of momentum space

2.3.1 Semi-discrete Wigner equation

The Wigner function (2.2) is defined with the Wigner transform (2.1) calculated over an infinite range. However, the finite dimensions of the simulation domain impose bounds on the variables defined by (2.3) such that the maximum value that s can attain is limited by the dimensions of the device (L_dev). Therefore, the Wigner function (2.2) must be calculated over finite dimensions:

∫ L∕2 fw (r,k,t) =-1 dse- i2k⋅sρ (r+ s,r- s,t), (2.31) L -L∕2

with the substitution of variables s
2

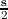→ s. The value L is termed the coherence length and can be chosen freely subject to certain physical and computational considerations, which are investigated in Chapter 4. An isotropic coherence length is chosen such that |L| = L.

A continuous function f(s) can be written as a Fourier series:

∑∞ i2πns- f (s) = Ane L , (2.32) n=-∞

where the Fourier coefficients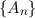 {An }

are given by

∫ L∕2 An = -1 dsf (s)e- i2πLns. (2.33) L -L∕2

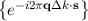Therefore, a finite value of L requires k to become discretized to form a complete orthogonal basis set { -i2πqΔk⋅s}
e

, where q is an integer multi-index and Δk = -π
L

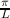, which denotes the resolution of the discretized wavevector.

From the above considerations, the discrete Fourier transform (DFT) follows, such that

1-∑ - iqΔk⋅s fw (r,q Δk,t) = L e ρ(r+ s,r - s,t) , (2.34) q

where Δk is, henceforth, omitted from the function arguments for brevity. Applying the same arguments to (2.11) yields:

( ∂ ℏqΔk ) ∑ ( ′) ( ′ ) ∂t + -m-*-∇r fw (r,q,t)w = Vw r,q - q fw r,q,t , (2.35) q′

The Wigner potential (which may also be time-dependent) is defined accordingly as

∫ L -1-- ∕2 -i2qΔk⋅s VW (r,q) ≡ iℏL -L∕2dse δV (2.36) δV (s;r) ≡ V (r+ s) - V (r- s). (2.37)

The equations (2.35) - (2.36) define the semi-discrete Wigner equation, which has been the subject of detailed mathematical analyses [66, 67].

[next] [prev] [prev-tail] [front] [up]