Subsections

• 5.2.1 Measurement of Breakdown
• 5.2.2 Models
  • 5.2.2.1 Anode Hole Injection Model
  • 5.2.2.2 Electron Trap Generation Model
  • 5.2.2.3 Percolation Model

5.2 Dielectric Wearout and Breakdown

The proper operation of MOS transistors relies on the insulating properties of the dielectric layer. Each dielectric material has a maximum electric field it can intrinsically sustain (dielectric strength). Applying a higher field leads to breakdown which destroys the insulating properties and allows current to flow. At lower electric fields the insulator can wear-out after some time and finally break down completely. This time-dependent dielectric breakdown (TDDB) is a very important reliability aspect for MOS structures [56].

For dielectric breakdown two scenarios are distinguished, extrinsic and intrinsic breakdown. Extrinsic breakdown is due to defects in the dielectric which can be introduced during different processing steps while intrinsic breakdown is because of the nature of the dielectric itself. It occurs at a certain electric field, defining the dielectric strength. As the insulating layers are getting thinner the probability of an external defect and therefore the probability of an extrinsic failure is decreasing. Hence intrinsic failure is the most likely problem for today's dielectrics.

5.2.1 Measurement of Breakdown

For thicker oxides, above 6nm, the time to breakdown can be defined as the moment when the oxide layer abruptly loses its insulating properties. This is called a hard breakdown and can be detected as a large jump in the current-time or voltage-time curve, depending whether constant voltage or constant current stress has been applied [57].

For very thin dielectrics and lower stress voltages, especially in large area capacitors, a soft breakdown is possible, which is very difficult to detect in the output curve as it changes only slightly. A significant change can be found in the gate current noise after soft breakdown. Therefore a breakdown detection method based on measurement of the increasing noise has been proposed [58].

5.2.2 Models

Several models have been proposed to characterize dielectric wearout and breakdown. Their target is to explain the mechanisms involved in dielectric degradation.

5.2.2.1 Anode Hole Injection Model

The anode hole injection model [59,60] suggests that electrons that tunnel through the dielectric can, when reaching the anode, transfer their excess energy to an electron deep in the valence band of the anode. This electron is promoted to the lower edge of the conduction band leaving a hot hole behind. These hot holes can then tunnel back into the dielectric generating oxide traps. The model suggests that these traps increase the current density through the dielectric due to trap-assisted tunneling (Section 5.3.2) leading to a runaway process followed by dielectric breakdown.

According to this model breakdown occurs when a critical hole fluence 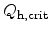is reached. It has been shown that for a 11nm oxide 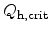is about 0.1 C/cm$^2$ [59]. However, it has been observed that this number decreases for thinner oxides [60,61] which cannot be explained by the model. There is also no physical explanation for the link between the breakdown event and the critical hole fluence.

5.2.2.2 Electron Trap Generation Model

The electron trap generation model claims a critical electron trap density (CETD) generated during stress to be necessary to trigger oxide breakdown. It presents the breakdown event as the formation of a conducting path of traps connecting the cathode to the anode [62,63,64,65].

Experiments show, though, that at thinner dielectrics the CETD for breakdown is decreased [61,60,66]. This is in contradiction with the electron trap generation model which predicts a critical trap density independent of the oxide thickness.

Figure 5.3: Schematic illustration of the percolation model for intrinsic oxide breakdown simulations. It is based on trap generation and conduction via these traps. A breakdown path is formed by spheres connecting anode and cathode.

5.2.2.3 Percolation Model

The breakdown model proposed by Degraeve et al. [66] is based on the percolation concept. It links both the anode hole injection model and the electron trap generation model. Degraeve et al. showed that the electron trap generation is correlated with the generated hole fluence and not with the oxide field and thickness. This implies that either the correlation is casual, i.e. holes are involved in the generation of traps, or that holes and traps are both related to a common parameter, which, for example, can be the energy of the injected electrons at the anode.

Figure 5.3 illustrates the percolation concept. During stress electron traps are generated in the dielectric at random positions. Around these traps, spheres with a constant radius 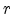$r$ are defined. These spheres give the conductive area around the traps. The radius is the only free parameter of the model. As soon as cathode and anode are connected by overlapping spheres, a conducting path is formed and the breakdown condition is reached. The critical electron trap density (CETD) can now be calculated as the number of traps divided by the volume of the simulated dielectric.

The percolation model predicts that for decreasing oxide thickness the CETD decreases, and due to the direct correlation also 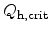. This is in perfect agreement with experimental findings [61,60,66]. So thinner oxides have a weaker ``hole fluence immunity''. This is an intrinsic property of the breakdown mechanism and is due to the lower number of traps necessary to form a conducting path through the dielectric. The second finding from the percolation model is the enhanced statistical spread of oxide breakdown for thinner oxides. As for thinner oxides only a few traps are necessary to form a conducting path, the statistical spread on the trap density is larger.