4.9 Surface Extraction

For visualization or further processing an explicit surface representation is more convenient than the implicit LS representation. To obtain a line segmentation or a triangulation from the LS function, the marching squares or the marching cubes algorithm [70] can be applied in two or three dimensions, respectively. The grid cells are processed in sequential order. If all corner grid points have the same LS sign, the surface does not intersect the cell. If there are any grid points with different signs, a surface segmentation is set up for the corresponding cell. The surface vertices are obtained as the intersection points of the zero LS with the cell edges. The surface elements of a cell are obtained using a predefined lookup table from the LS signs of all its corners. Since all grid cells need to be processed, the original algorithm scales with the domain size.

However, if the H-RLE data structure is used to represent the LS function, this algorithm can be implemented with linear complexity with respect to the number of defined grid points, which is usually proportional to the surface area. A cell-shaped stencil of 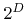$2^{D}$ iterators is used and moved across the H-RLE data structure. These iterators enable easy access to the LS values at all corners, as needed to determine any intersection points on edges. However, references to all new vertices on edges, which are attached to cells that have not been processed yet, are buffered in queues. When the stencil of iterators reaches a neighboring cell, according to the lexicographical processing order, vertices on edges, which have already been computed can easily be found. This avoids adding the same vertex twice and ensures the connectivity of all surface elements throughout neighboring grid cells.