




VLSICAP is a collection of FORTRAN programs which perform capacitance analysis in two passes. In a first pass, MESHCP automatically converts a user's description of the simulation region into a finite element mesh. The second program VLSICP uses this discretization to solve Equations 8.1-8.6 numerically.
Triangular finite elements with biquadratic basis functions are employed [Zien91][Zien89][Bath90][Schw91]. The initial grid is adaptively refined without any user interaction in order to distribute the local discretization error evenly on the simulation region and keep it below a certain limit. In other words, the grid is refined where the solution varies rapidly to achieve a better approximation. A run of VLSICP yields potential and field distribution, electrostatic field energy, surface and space charges. Additionally, the coefficients of capacitance are calculated for the multiconductor system under consideration.
VLSICAP solves the two-dimensional POISSON equation
with the respective charge densities being in the dielectric (insulator)
in the p-type semiconductor
and in the n-type semiconductor
The doping profile is
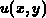 is the electrostatic potential, and
is the electrostatic potential, and 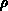 is the space charge
density. As can be seen in Equation 8.4 and 8.6, BOLTZMANN
statistics are used to model densities of electrons
is the space charge
density. As can be seen in Equation 8.4 and 8.6, BOLTZMANN
statistics are used to model densities of electrons  and holes
and holes 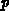 .
.
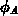 and
and 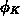 are the external potentials applied to the conductor
which contacts the p- and n-type semiconductor, respectively. Constants
involved are electronic charge
are the external potentials applied to the conductor
which contacts the p- and n-type semiconductor, respectively. Constants
involved are electronic charge 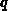 , intrinsic number
, intrinsic number 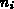 , absolute
temperature
, absolute
temperature 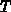 and BOLTZMANN's constant
and BOLTZMANN's constant 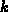 .
.  is the
dielectric constant of the insulator or semiconductor.
is the
dielectric constant of the insulator or semiconductor. 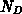 and
and 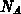 are
the donor and acceptor concentrations.
are
the donor and acceptor concentrations.
The set of equations Equations 8.1-8.6 is only valid under the
following two assumptions: There is no current flow in the semiconductor
segments, since just the POISSON equation is solved , and each semiconductor segment is contacted by exactly one contact,
since only then the quasi-fermi potentials for electrons and holes can be
substituted with the directly applied potentials in Equation 8.4 and
8.6
, and each semiconductor segment is contacted by exactly one contact,
since only then the quasi-fermi potentials for electrons and holes can be
substituted with the directly applied potentials in Equation 8.4 and
8.6 .
.
Using the quasi-fermi potentials 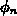 and
and 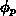 , the semiconductor
current density equations can be written as [Sze81]
, the semiconductor
current density equations can be written as [Sze81]
The first assumption implies that 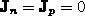 , and
, and 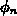 and
and 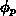 have therefore to be constant across the whole semiconductor
region. Using the quasi-fermi potential definitions again in the BOLTZMANN relation, the product of the carrier densities becomes [Sze81]
have therefore to be constant across the whole semiconductor
region. Using the quasi-fermi potential definitions again in the BOLTZMANN relation, the product of the carrier densities becomes [Sze81]
The electrostatic potential difference across the depletion layer is now 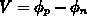 , and under the second assumption stated above, this difference
is equal to the difference of the externally applied bias potentials, which is
the reason for the substitution mentioned above.
, and under the second assumption stated above, this difference
is equal to the difference of the externally applied bias potentials, which is
the reason for the substitution mentioned above.
The shape of the two-dimensional user-defined simulation region may be arbitrary and is bounded by polygons. Multiply connected regions (containing ``holes'') are permitted. The simulation area represents the cross-section of an integrated circuit structure and may consist of semiconductor, dielectrics and contacts. Equations 8.1-8.7 are solved numerically by the finite element approach. Nonlinear problems are tackled by a modified NEWTON method [Stra85].
The electrostatic charges on conductor surfaces and space charges in
semiconductor regions are computed from the potential distribution 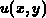 in
order to find the coefficients of capacitance for the multiconductor system
investigated.
in
order to find the coefficients of capacitance for the multiconductor system
investigated.
These coefficients of capacitance are calculated by solving the linear equation system
for the unknown vector of capacitances 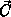 .
.
The field energies computed in multiple runs of VLSICP are combined into a
vector 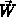 , the entries of the coefficient matrix
, the entries of the coefficient matrix 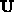 are
calculated from the boundary condition pattern for the conductors.
are
calculated from the boundary condition pattern for the conductors.



