Next: 3.1.3 Simulating Oxide Growth Up: 3.1 Thermal Oxidation Simulators Previous: 3.1.1 History of Oxidation
A visco-elastic oxide growth model has been developed at our institute using FEM as the simulation environment [80]. The model is three-dimensional and does not rely on a simple expression for the interface motion, but rather relies on calculations of oxidant diffusion and oxide volume expansion in three dimensions to move the FEM mesh appropriately. A major limitation of FEM analysis is related to the mesh used for simulations. As either the time or space increments are decreased, or the mesh is made finer, the number of calculations necessary to simulate oxide growth can increase by a factor dependent on the model itself [34], [159]. Some models also do not account for orientation dependence adequately or the error can be a non-linear function which can amplify significantly with further iterations [229].
The model presented in [80] is based on a few main equations. The first equation is meant to describe oxidant diffusion
| (72) |
 is the
Laplace operator,
is the
Laplace operator,
| (73) |
The next equation is meant to deal with the dynamics of ![]()
 |
(74) |
The volume increase of the generating oxide occurs successively and not abruptly because of the diffuse interface concept. A volume
increase of the oxidized material is calculated using the ![]() and
and ![]() values. After a given time
values. After a given time ![]() , the normalized
additional volume is given by
, the normalized
additional volume is given by
Since the principal axis components of the residual strain tensor
![]() are linearly proportional
to
are linearly proportional
to
![]() in the form
in the form
 |
(76) |
 |
(78) |
The effective shear modulus ![]() can be added to
can be added to
![]() to handle elastic and visco-elastic materials.
For elastic materials
to handle elastic and visco-elastic materials.
For elastic materials
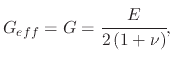 |
(79) |
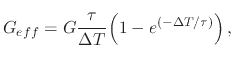 |
(80) |