A.1 Transport under a Velocity-Dependent Acceleration
This section is devoted to describe the derivation of the equations of motion (5.3)-(5.12) for a droplet experiencing a
force in the direction of its motion such as gravity as well as forces working against its motion such as the thermophoretic force and the
velocity-dependent Stokes force. For now, it is assumed that there is no influence from the electric force on the droplet motion.
The first step is to equate all forces acting on the droplet
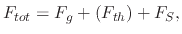 |
(208) |
where 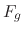 is the force due to gravity,
is the force due to gravity, 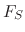 is the Stokes force, and the thermophoretic force
is the Stokes force, and the thermophoretic force 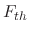 is
in brackets, because it is only included, when the droplet reaches the heat zone, and at that point, the
radius must be modified according to its evaporation. However, for the following derivations, a constant radius will be assumed. Therefore, when the
thermophoretic force is to be included, a smaller radius
is
in brackets, because it is only included, when the droplet reaches the heat zone, and at that point, the
radius must be modified according to its evaporation. However, for the following derivations, a constant radius will be assumed. Therefore, when the
thermophoretic force is to be included, a smaller radius 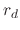 is carried through the equations. The forces can be converted to droplet acceleration
using
is carried through the equations. The forces can be converted to droplet acceleration
using
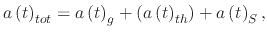 |
(209) |
where
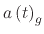 ,
,
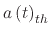 , and
, and
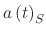 are the droplet accelerations due to gravity, the thermophoretic force,
and the Stokes force, respectively. Since
are the droplet accelerations due to gravity, the thermophoretic force,
and the Stokes force, respectively. Since
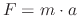 , then
, then
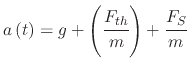 |
(210) |
and the droplet mass 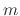 is given by
is given by
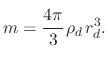 |
(211) |
The explicit equation for the droplet acceleration can be derived by substituting the relevant forces and the droplet mass 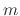 into (A.3)
into (A.3)
![$\displaystyle a\left(t\right)=\left[g+\left(-\frac{27\,\eta_{a}^{2}\,\kappa_{a}...
...r^{2}}\right)\right]- \cfrac{9\,\eta_{a}}{2\,\rho_{d}\,r^{2}}\,v\left(t\right),$](img880.png) |
(212) |
where the meaning and values for the droplet and ambient parameters in (A.5) can be found in Table 6.1.
In order to simplify the derivation, all constant values will be grouped together and only two constants will remain in the form of the
independent constant 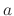 and constant
and constant 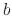 , which relates the velocity dependence of the acceleration
, which relates the velocity dependence of the acceleration
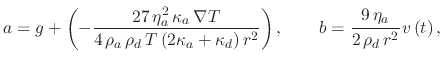 |
(213) |
allowing for (A.5) to be rewritten as
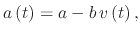 |
(214) |
The solution to (A.7) is found by first noting that it is a differential equation
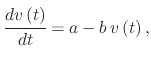 |
(215) |
which can be re-written in the form
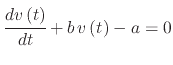 |
(216) |
and converted into Euler's characteristic equation
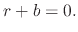 |
(217) |
This characteristic equation only has one root, 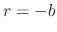 , meaning the velocity can be solved by writing
, meaning the velocity can be solved by writing
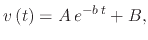 |
(218) |
where 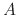 and
and 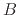 are constants. In order to find
are constants. In order to find 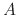 and
and 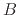 , two assumptions must be made: the initial velocity
, two assumptions must be made: the initial velocity
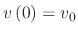 is known
and at some time
is known
and at some time 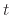 , the velocity will reach a terminal velocity due to the equivalent and opposite forces acting on the droplet, meaning
, the velocity will reach a terminal velocity due to the equivalent and opposite forces acting on the droplet, meaning
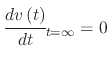 . Therefore, when
. Therefore, when 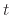 approaches infinity,
approaches infinity,
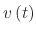 from (A.11) approaches
from (A.11) approaches 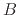 , meaning that
, meaning that
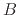 is the terminal velocity
is the terminal velocity
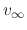 . This can be substituted into (A.7) to obtain
. This can be substituted into (A.7) to obtain
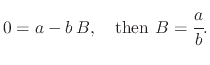 |
(219) |
Now that 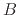 and
and
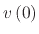 are known, they can be substituted into (A.11) to find
are known, they can be substituted into (A.11) to find 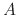
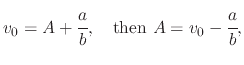 |
(220) |
giving the final description for the velocity of the droplet at any time 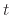
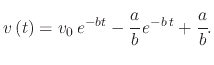 |
(221) |
In order to find the displacement of the droplet under the given forces, (A.14) can be integrated from 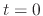 , when the
initial displacement
, when the
initial displacement 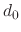 is set to 0
is set to 0
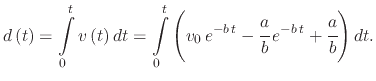 |
(222) |
resulting in
![$\displaystyle d\left(t\right)=\left[-\cfrac{v_{0}}{b}\,e^{-b\,t}+\cfrac{a}{b^{2}}\,e^{-b\,t}+\cfrac{a}{b}\,t\right]_{0}^{t}.$](img898.png) |
(223) |
The displacement is then given by
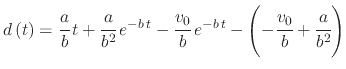 |
(224) |
or
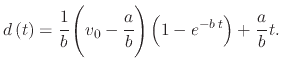 |
(225) |
The time 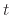 is needed in order to calculate the droplet displacement. As the droplet travels through the ambient, it is much easier
to calculate the time required for the droplet to reach the wafer followed by the calculation of the radial direction displacement. This would make simulations much
quicker than a discretization of the time
is needed in order to calculate the droplet displacement. As the droplet travels through the ambient, it is much easier
to calculate the time required for the droplet to reach the wafer followed by the calculation of the radial direction displacement. This would make simulations much
quicker than a discretization of the time 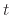 in order to follow the droplet trajectory. The time is found by inverting (A.18)
in order to follow the droplet trajectory. The time is found by inverting (A.18)
![$\displaystyle t=\cfrac{a\,W\left[\cfrac{\left(a-b\,v_{0}\right)\cdot e^{1-\frac...
...(v_{0}+b\,d(t)\right)}{a}}}{a}\right]-a+b\,v_{0}+b^{2}\,d\left(t\right)}{a\,b},$](img901.png) |
(226) |
where
![$ W\left[\cdot \right]$](img617.png) is the Lambert-W function which is solved iteratively and is defined by
is the Lambert-W function which is solved iteratively and is defined by
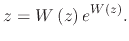 |
(227) |
L. Filipovic: Topography Simulation of Novel Processing Techniques
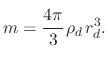
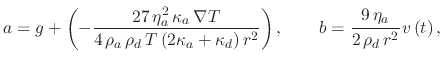
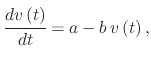
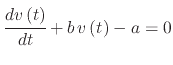
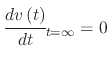 . Therefore, when
. Therefore, when 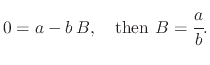
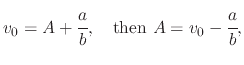
![]() , when the
initial displacement
, when the
initial displacement ![]() is set to 0
is set to 0
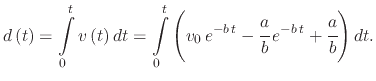
![$\displaystyle d\left(t\right)=\left[-\cfrac{v_{0}}{b}\,e^{-b\,t}+\cfrac{a}{b^{2}}\,e^{-b\,t}+\cfrac{a}{b}\,t\right]_{0}^{t}.$](img898.png)
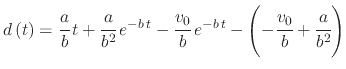
![]() is needed in order to calculate the droplet displacement. As the droplet travels through the ambient, it is much easier
to calculate the time required for the droplet to reach the wafer followed by the calculation of the radial direction displacement. This would make simulations much
quicker than a discretization of the time
is needed in order to calculate the droplet displacement. As the droplet travels through the ambient, it is much easier
to calculate the time required for the droplet to reach the wafer followed by the calculation of the radial direction displacement. This would make simulations much
quicker than a discretization of the time ![]() in order to follow the droplet trajectory. The time is found by inverting (A.18)
in order to follow the droplet trajectory. The time is found by inverting (A.18)
![$\displaystyle t=\cfrac{a\,W\left[\cfrac{\left(a-b\,v_{0}\right)\cdot e^{1-\frac...
...(v_{0}+b\,d(t)\right)}{a}}}{a}\right]-a+b\,v_{0}+b^{2}\,d\left(t\right)}{a\,b},$](img901.png)