A.2 Transport under a Velocity- and Displacement-Dependent Acceleration
When the acceleration of a droplet also depends on the droplet's position in a simulation environment, or the displacement from its original position, such as is
the case with the application of an electric force to a droplet's transport, the total force experienced by a droplet becomes
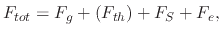 |
(228) |
where 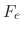 is the electric force and the acceleration becomes
is the electric force and the acceleration becomes
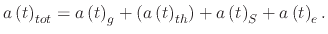 |
(229) |
Acceleration due to the applied electric field is modeled as a linear displacement-dependent acceleration from (5.28)
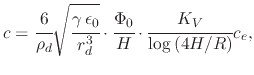 |
(230) |
while acceleration due to gravity and the Stokes component of the acceleration remain the same from Section A.1.
Therefore, the following equation must be solved to find the droplet displacement after time 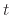
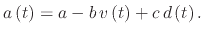 |
(231) |
The equation can be re-written into a standard quadratic form, which is easier to solve
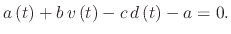 |
(232) |
Noting that
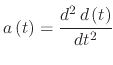 ,
,
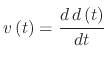 , and
, and
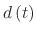 is the displacement.
is the displacement.
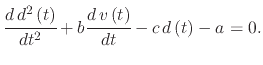 |
(233) |
Using the Laplace method for solving differential equations, the characteristic equation, (A.26) can be re-written using
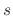 to depict a derivation step and
to depict a derivation step and 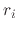 to depict the roots of equations. Assuming the initial velocity
to depict the roots of equations. Assuming the initial velocity 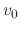 and initial displacement
and initial displacement 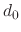 ,
(A.26) becomes
,
(A.26) becomes
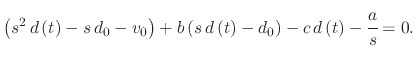 |
(234) |
Multiplying by 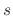 gives
gives
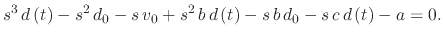 |
(235) |
Isolating for
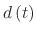 gives
gives
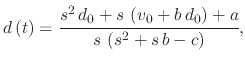 |
(236) |
which is then split according to the numerator's power of 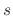 using partial fractional decomposition
using partial fractional decomposition
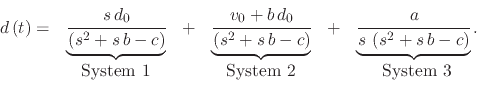 |
(237) |
The roots of the equation can be found by finding 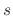 values for which (A.30) is invalid, or infinity. These roots are
values for which (A.30) is invalid, or infinity. These roots are
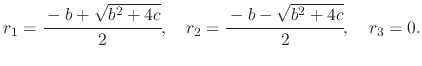 |
(238) |
In order to find the final equation for the displacement
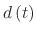 , a solution to each system in (A.30) must be found and added together
, a solution to each system in (A.30) must be found and added together
- System 1
System 1 is set up such that the two roots are separated
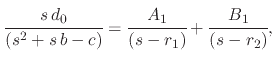 |
(239) |
where 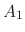 and
and 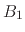 are parameters to solve the displacement due to System 1
are parameters to solve the displacement due to System 1
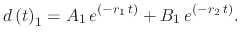 |
(240) |
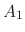 and
and 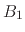 are found using (A.32)
are found using (A.32)
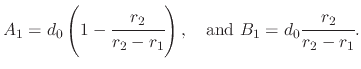 |
(241) |
- System 2
Similar to System 1, System 2 is set up, separating the effects from the two roots
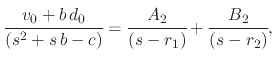 |
(242) |
where 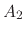 and
and 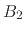 are parameters to solve the displacement due to System 2
are parameters to solve the displacement due to System 2
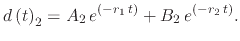 |
(243) |
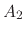 and
and 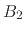 are found using (A.35)
are found using (A.35)
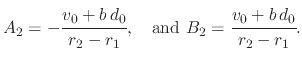 |
(244) |
- System 3
System 3 has an additional root involvement from the presence of 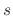 in the denominator, so the system is set up as
in the denominator, so the system is set up as
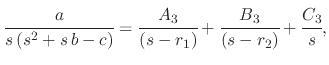 |
(245) |
where 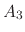 ,
, 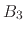 , and
, and 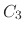 are parameters to solve the displacement due to System 3
are parameters to solve the displacement due to System 3
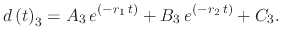 |
(246) |
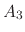 ,
, 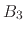 , and
, and 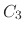 are found using (A.38)
are found using (A.38)
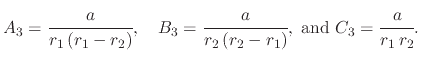 |
(247) |
After combining all three systems, the equation which governs the displacement at time 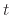 due to velocity and displacement-dependent acceleration
is given by
due to velocity and displacement-dependent acceleration
is given by
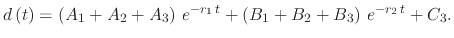 |
(248) |
It should be noted that, if the initial displacement is set to 0, then 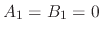 . Similarly, if the initial velocity is also set
to 0, then
. Similarly, if the initial velocity is also set
to 0, then 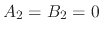 , significantly reducing the complexity of the problem.
, significantly reducing the complexity of the problem.
L. Filipovic: Topography Simulation of Novel Processing Techniques
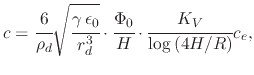
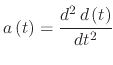 ,
,
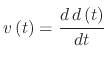 , and
, and
![]() to depict a derivation step and
to depict a derivation step and ![]() to depict the roots of equations. Assuming the initial velocity
to depict the roots of equations. Assuming the initial velocity ![]() and initial displacement
and initial displacement ![]() ,
(A.26) becomes
,
(A.26) becomes
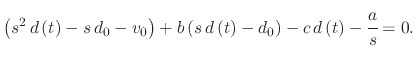
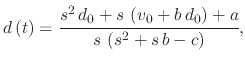
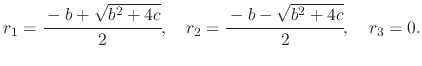
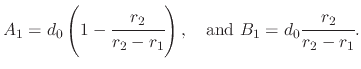
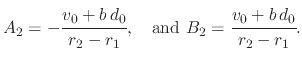
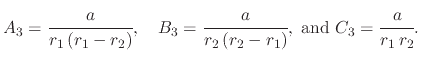
![]() due to velocity and displacement-dependent acceleration
is given by
due to velocity and displacement-dependent acceleration
is given by