B. Generating a Distribution for the Droplet Radius
The random distribution for the droplet radius for the ESD spray pyrolysis model in (6.1) is derived in this section.
The volume fraction is evenly distributed along
the droplets whose radii range from
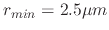 to
to
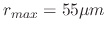 . Therefore, the first step is to relate the radius distribution linearly to
a value
. Therefore, the first step is to relate the radius distribution linearly to
a value
![$ x\in\left[0,1\right]$](img935.png) so that as
so that as  goes from 0 to 1,
goes from 0 to 1,  goes from
goes from  to
to 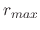 :
:
![$\displaystyle r_{d}\left(x\right)=\left(r_{max}-r_{min}\right)x+r_{min},\quad\textrm{where }x\in\left[0,1\right].$](img938.png) |
(249) |
Next, the assertion is made that 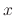 represents the evenly distributed volume number fraction, or normalized volume
represents the evenly distributed volume number fraction, or normalized volume  .
Using the equation for the volume of a sphere, the relationship between volume and radius is established as
.
Using the equation for the volume of a sphere, the relationship between volume and radius is established as
 |
(250) |
Therefore, when the volume is evenly distributed, the effect on the radius will be
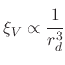 . Initially, it might be counter-intuitive
to note the inverse relationship since
. Initially, it might be counter-intuitive
to note the inverse relationship since
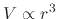 . However, when a volume of
. However, when a volume of  is distributed for a radius
is distributed for a radius  m, then
m, then
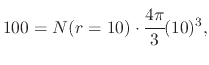 |
(251) |
where 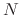 is the number fraction, resulting in
is the number fraction, resulting in  . When the same volume is distributed for droplets of a radius
. When the same volume is distributed for droplets of a radius  m, then the calculation above
leads to the number fraction
m, then the calculation above
leads to the number fraction
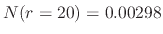 , which is 8 times less, or
, which is 8 times less, or
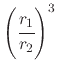 times less.
times less.
Now we know that the radius distribution should follow the equation
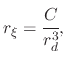 |
(252) |
where  is a normalization constant which must be found,
is a normalization constant which must be found, 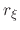 is the randomly distributed radius, and
is the randomly distributed radius, and 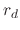 is the radius relating
is the radius relating
 and
and 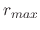 to an even volume distribution
to an even volume distribution
![$ \xi_V\in\left[0,1\right]$](img952.png) from (B.1)
from (B.1)
![$\displaystyle r_{\xi}=\cfrac{C}{\left[\left(r_{max}-r_{min}\right)\xi_V+r_{min}\right]^{3}}.$](img953.png) |
(253) |
Inverting (B.5) to solve for  allows to find the CPD function
allows to find the CPD function
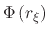
![$\displaystyle \Phi\left(r_{\xi}\right)=\xi_V=\cfrac{1}{r_{max}-r_{min}}\left[\left(\cfrac{C}{r_{\xi}}\right)^{1\slash3}-r_{min}\right].$](img956.png) |
(254) |
The derivative of (B.6) gives the PDF
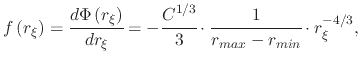 |
(255) |
where it can be noted that the last  term from (B.6) has disappeared. The only non-constant term in (B.7) is
term from (B.6) has disappeared. The only non-constant term in (B.7) is
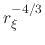 , therefore a replacement constant, which will be the new normalization constant is introduced for simplicity
, therefore a replacement constant, which will be the new normalization constant is introduced for simplicity
 |
(256) |
and (B.7) can be rewritten to
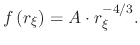 |
(257) |
Using the PDF from (B.9), we can now proceed to find the normalized distribution 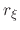 , but first the normalization constant
, but first the normalization constant 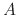 must be
found by integrating (B.9) with respect to
must be
found by integrating (B.9) with respect to  from
from  to
to 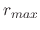 and equating the integral to 1
and equating the integral to 1
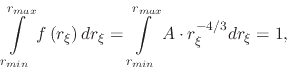 |
(258) |
which can be solved to
![$\displaystyle -3A\left[\left(\cfrac{1}{r_{max}}\right)^{1\slash3}-\left(\cfrac{1}{r_{min}}\right)^{1\slash3}\right]=1,$](img962.png) |
(259) |
giving the normalization constant 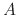
![$\displaystyle A=-\cfrac{1}{3\left[r_{max}^{-1\slash3}-r_{min}^{-1\slash3}\right]}$](img963.png) |
(260) |
and the normalized PDF
![$\displaystyle f\left(r_{d}\right)=-\cfrac{1}{3\left[r_{max}^{-1\slash3}-r_{min}^{-1\slash3}\right]}\cdot r_{d}^{-4\slash3}.$](img964.png) |
(261) |
Now one can integrate the normalized PDF from  to
to  to find the CPD
to find the CPD
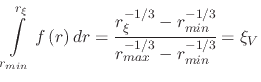 |
(262) |
and invert the CPD to find the quantile function and solve for 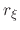
![$\displaystyle r_{\xi}=\left\{ \xi_V\cdot\left[\left(r_{max}\right)^{-1\slash3}-...
...{min}\right)^{-1\slash3}\right]+\left(r_{min}\right)^{-1\slash3}\right\} ^{-3},$](img966.png) |
(263) |
which gives the equation for the radius distribution  between
between  and
and  when the volume number fraction
when the volume number fraction
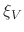 is evenly distributed and
is evenly distributed and
![$ \xi_V\in\left[0,1\right]$](img952.png) .
.
L. Filipovic: Topography Simulation of Novel Processing Techniques
![]() to
to
![]() . Therefore, the first step is to relate the radius distribution linearly to
a value
. Therefore, the first step is to relate the radius distribution linearly to
a value
![]() so that as
so that as ![]() goes from 0 to 1,
goes from 0 to 1, ![]() goes from
goes from ![]() to
to ![]() :
:
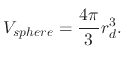
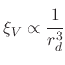 . Initially, it might be counter-intuitive
to note the inverse relationship since
. Initially, it might be counter-intuitive
to note the inverse relationship since
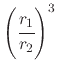 times less.
times less.
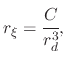
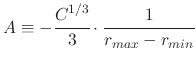
![]() , but first the normalization constant
, but first the normalization constant ![]() must be
found by integrating (B.9) with respect to
must be
found by integrating (B.9) with respect to ![]() from
from ![]() to
to ![]() and equating the integral to 1
and equating the integral to 1
![$\displaystyle -3A\left[\left(\cfrac{1}{r_{max}}\right)^{1\slash3}-\left(\cfrac{1}{r_{min}}\right)^{1\slash3}\right]=1,$](img962.png)
![$\displaystyle A=-\cfrac{1}{3\left[r_{max}^{-1\slash3}-r_{min}^{-1\slash3}\right]}$](img963.png)
![$\displaystyle f\left(r_{d}\right)=-\cfrac{1}{3\left[r_{max}^{-1\slash3}-r_{min}^{-1\slash3}\right]}\cdot r_{d}^{-4\slash3}.$](img964.png)
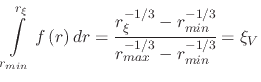
![$\displaystyle r_{\xi}=\left\{ \xi_V\cdot\left[\left(r_{max}\right)^{-1\slash3}-...
...{min}\right)^{-1\slash3}\right]+\left(r_{min}\right)^{-1\slash3}\right\} ^{-3},$](img966.png)