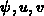 ) über, der anstelle der
Trägerkonzentrationen
) über, der anstelle der
Trägerkonzentrationen 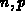 die diesen zugeordneten
SLOTBOOM-Variablen [72]
die diesen zugeordneten
SLOTBOOM-Variablen [72]  und
und  enthält:
enthält:




Löst man die Poissongleichung als Teil eines gekoppelten Gesamtsystems von Differentialgleichungen, wie das bei der Halbleitersimulation der Fall ist, so muß man die starke Abhängigkeit der Raumladung vom Potential berücksichtigen.
Will man das Gesamtsystem entkoppelt lösen (also jeden Gleichungstyp für sich), so hat diese Abhängigkeit besonders ungünstigen Einfluß, weil die Auswirkungen des Potentials auf die Trägerkonzentrationen in der alleinstehenden Poissongleichung a priori nicht enthalten sind. Besonders in Gebieten mit hohen Trägerkonzentrationen (an Kontakten, in hochdotierten Zonen) führt das zu Schwingungen und zu Divergenz des Gesamtsystems.
Im stationären Fall und im transienten Fall können gegen diese Instabilität strukturell ähnliche Maßnahmen unternommen werden. Der transiente Fall wird in Abschnitt 3.4 behandelt, der stationäre hier.
Nach H. GUMMEL [29] kann man im stationären Fall bessere Stabilität eines entkoppelten Verfahrens erzielen, indem man die annäherungsweise exponentielle Variation der Trägerkonzentrationen mit dem Potential in der Poissongleichung berücksichtigt.
Man geht für die Formulierung der Poissongleichung zu dem
Variablensatz (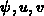 ) über, der anstelle der
Trägerkonzentrationen
) über, der anstelle der
Trägerkonzentrationen 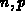 die diesen zugeordneten
SLOTBOOM-Variablen [72]
die diesen zugeordneten
SLOTBOOM-Variablen [72]  und
und  enthält:
enthält:
Dabei ist 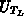 die Temperaturspannung, die sich aus der
Gittertemperatur ergibt:
die Temperaturspannung, die sich aus der
Gittertemperatur ergibt:
Man kann nun die Ableitung der Raumladung 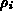 nach dem lokalen
Potential
nach dem lokalen
Potential 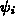 an einem Gitterpunkt
an einem Gitterpunkt 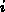 bestimmen:
bestimmen:
Mit dem diskreten Boxintegral über diese Ableitung, das in Gleichung 3.8 enthalten ist,
kann man die partiellen Ableitungen in 3.15 zu quasi totalen ergänzen. Für den Inkrementsvektor ergibt sich dann folgende neue Gleichung:
Weil die rein exponentiellen Abhängigkeiten nicht völlig korrekt sind (das wären sie nur ohne Stromfluß und mit allen Ladungsträgern auf Gittertemperatur), wird die Gleichung 3.20 die Änderungen in den Ladungsträgerkonzentrationen und in der Raumladung nicht genau antizipieren. Trotzdem macht diese Modifikation oft das entkoppelte Lösungsverfahren überhaupt erst konvergent. Die Zusatzterme in 3.20 stärken nämlich die Diagonale des Gleichungssystems und vermindern damit ein Überschwingen der Lösung für das Potential.
Im Rahmen des entkoppelten Verfahrens ist nach einer Änderung des
Potentials um 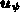 die Poissongleichung (3.11) nicht erfüllt, weil die vorweggenommene Änderung der Raumladung
noch nicht eingetreten ist; dafür ist es erst notwendig, die
Kontinuitätsgleichungen zu lösen. Das entkoppelte
Iterationsverfahren mit der Poissongleichung aus (3.20)
bezeichnet man als GUMMEL-Schema [29].
die Poissongleichung (3.11) nicht erfüllt, weil die vorweggenommene Änderung der Raumladung
noch nicht eingetreten ist; dafür ist es erst notwendig, die
Kontinuitätsgleichungen zu lösen. Das entkoppelte
Iterationsverfahren mit der Poissongleichung aus (3.20)
bezeichnet man als GUMMEL-Schema [29].
Es soll hier noch darauf hingewiesen werden, daß die beschriebenen Umformungen zwar das lineare Gleichungssystem verändern (mit dem Ziel einer beschleunigten oder überhaupt erst ermöglichten Konvergenz des nichtlinearen Iterationsschemas), daß aber dadurch die nichtlinearen Gleichungen, die in den Kontrollfunktionen ausgedrückt werden, selbstverständlich nicht verändert werden. Wenn also eine Lösung gefunden ist, die das Residuum einer Gleichung verschwinden läßt (auf welchem Weg auch immer), dann ist die Gleichung tatsächlich korrekt gelöst.
Man kann das Gesamtsystem von Gleichungen auch gekoppelt lösen.
In diesem Fall ist es nicht notwendig (und auch nicht erlaubt), die
Zusatzterme aus (3.20) zu verwenden.
Würde man die Zusatzterme in das Gleichungssystem einbauen, hätte
man die Ableitungen nach dem Potential in der Poissongleichung mit dem
Variablensatz (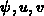 ) ausgedrückt, in den anderen
Gleichungen aber mit (
) ausgedrückt, in den anderen
Gleichungen aber mit (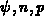 ), und die Matrix des
Gleichungssystems wäre inkonsistent aufgebaut. Im gekoppelten System
ist der Einfluß des Potentials auf die Raumladung
), und die Matrix des
Gleichungssystems wäre inkonsistent aufgebaut. Im gekoppelten System
ist der Einfluß des Potentials auf die Raumladung 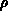 über die
Trägerkonzentrationen indirekt ohnehin enthalten.
über die
Trägerkonzentrationen indirekt ohnehin enthalten.
Trotzdem ist auch hier eine ähnliche Modifikation möglich: Man kann, ohne das Gesamtsystem zu verändern, eine Variablentransformation durchführen, wie sie in [4] von ASCHER et al. beschrieben wurde. Diese Transformation hat auf die Poissongleichung exakt denselben Effekt wie die Terme in (3.20), bringt allerdings gleichzeitig die Kontinuitätsgleichungen in eine Form, in der die Differentialoperatoren für das Potential verschwinden (Diagonalisierung nach ,,führenden Termen``). Obwohl der letztere Effekt bei veränderlichen Trägertemperaturen (also bei hydrodynamischen Gleichungen) nicht voll zustande kommt, weil die Differentialausdrücke von anderer Gestalt sind, ist dennoch im Experiment bei reinen Drift-Diffusionsansätzen wie bei hydrodynamischen Gleichungen eine radikale Verbesserung der Kondition (siehe Anhang B) der Systemmatrix zu beobachten. Die Transformation aus [4] wurde daher in das Simulationsprogramm eingebaut.



