4.4 Advancing Front Methods

The mesh is constructed by progressively adding mesh elements starting at the boundaries. This iteration results in a propagation of a front which is the border (internal boundary) between the meshed and the unmeshed region. The difficulty with this method lies in the merging of the advancing front. A new triangular/tetrahedral mesh element is added by inserting one new point^4.1. The location of this point is crucial and is determined by the following criteria.

• The quality of the resulting element.
• The desired mesh spacing given by the control space.
• Neighborhood constraints like other parts of the boundary/front.
• The point must be inside of the domain.

Figure 4.8: Various situations in two dimensions and different patterns depending on the angle 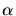$\alpha$.

Adjusting the location of a point to meet all of these criteria requires a very complex analysis of the surrounding region. A previously generated point which belongs to a different part of the front may have to be preferred. In such a case no new point will be created and the two parts of the front merge. This results in a decrease of the size of the active front. The final step of the mesh iteration is a full merge where no active front remains. A few example situations are depicted in Fig. 4.8. The last two criteria must be checked by extensive search algorithms and intersection tests.

• None of the created edges which are connected to the new point may intersect any edge/facet of the two-dimensional/three-dimensional front.
• None of the created facets containing the new point may intersect any edge of the three-dimensional front.
• The new element must not contain any other points.

In three dimensions the second test is required additionally to the first. All three cases are illustrated in Fig. 4.9. If a more or less ideal initial guess for the location of a new point fails the intersection tests, the question how to alter the position successfully will arise. Sacrifices with regard to element quality and mesh spacing have to be made. A background mesh as explained in Section 3.3 can be utilized to evaluate the neighborhood constraints and to help the decision process. For example a volume mesh of the boundary/front without internal mesh points, a boundary mesh, contains much required information like distances and closest neighbors. This ``background boundary mesh'' must be locally updated each time the front advances. A Delaunay mesh seems most suitable for such purposes and was integrated as a background boundary mesh into an advancing front method by [50] as already briefly discussed in Section 2.3.

Figure 4.9: Three necessary tests to avoid collisions in three dimensions. The arrows show the direction of the advancing front and the tetrahedron which is tested and built.

The surface mesh of the boundary from which the advancing front departs has a great influence on the volume mesh. A high quality surface triangulation is required for the generation of a tetrahedral mesh. Which and in what order the surface triangles are effectively used as launching seeds for the advancing front is another important opportunity to influence the final mesh. In fact, it is the advantage of advancing front methods that the elements near the boundary can be controlled directly. Protection layers around physically crucial boundaries can be constructed by departing from those boundaries with several very small stepsizes. However, orthogonality is not a priori guaranteed by the original advancing front method. Enhancements to the algorithm are needed to provide perpendicular and parallel grid lines near boundaries. Arbitrary thin layers pose no difficulties in theory, but in practice require intelligent mechanisms to evaluate the neighborhood constraints. The advancing front method produces fully unstructured meshes and allows general anisotropic mesh elements.