5.1 Tetrahedralization of a Point Set

Euler's formula is a fundamental corollary in homology theory and describes for three-dimensional complexes the relationship between the number of vertices $n$, the number of edges $e$, the number of facets $f$, and the number of solids $s$.

$$n - e + f - s = 0$$

The number of solids includes the infinite solid ``outside'' of the complex. In this sense all facets are boundaries between solids. For the example of a cube it becomes $(8-12+6-2=0)$. Splitting one facet of the cube into two triangles results in $(8-13+7-2=0)$. For a general tetrahedralization Euler's formula can be written as

$$n - e + t - T = 1$$

where $t$ is the number of triangles and $T$ the number of tetrahedra. Based on this equation simple bounds on the number of tetrahedra can be deduced

$$n-3 \leq T \leq \left( \begin{array}{c} n-1 \\ 2 \end{array} \right) - n_{hull} + 2$$

where $n_{hull}$ is the number of points on the convex hull. A detailed combinatorial analysis and the investigation of various types of tetrahedralizations with different characteristics, worst case scenarios, as well as construction algorithms can be found in [40].

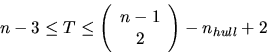
The three-dimensional Delaunay Triangulation is a special type of tetrahedralization[36]. In two dimensions a Delaunay Triangulation is known to minimize the largest circumcircle, to minimize the largest minimum-containment circle, and to maximize the minimum angle of all triangulations. The minimum-containment circle of a triangle is the smallest circle which contains the triangle. The circumcircle of an obtuse triangle is larger. The optimization of the angle seems to be due to the in two dimensions existing relation between edge length, circumcircle, and opposite angle (3.7). In three dimensions the Delaunay Triangulation is only known to minimize the largest minimum-containment sphere [15,130]. An important difference between two and three dimensions is the number of triangles/tetrahedra as a function of the number of points $n$. While the number of triangles in any triangulation grows with $O(n)$, the number of Delaunay tetrahedra in a tetrahedralization can grow with $O(n^{2})$ [123].