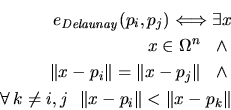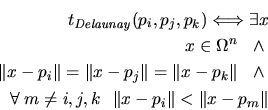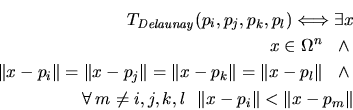


Next: 5.3 Algorithms for Constructing
Up: 5. Delaunay Triangulation
Previous: 5.1 Tetrahedralization of a
The definition of the Delaunay Triangulation is based on the Voronoi
diagram through the principle of duality (Fig. 5.1). Voronoi
diagrams and their application in an enormous amount of fields are
described in detail with many original references in [117].
Definition 5.1 (Voronoi)
Let
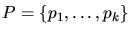 be a finite set of points in the
be a finite set of points in the
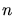 -dimensional space
-dimensional space 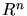 and their location vectors
and their location vectors
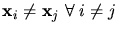 . The region
given by
is called Voronoi region (Voronoi box) associated with
. The region
given by
is called Voronoi region (Voronoi box) associated with 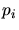 and
is said to be the Voronoi diagram of
and
is said to be the Voronoi diagram of 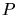 .
.
A Voronoi box is formed through the intersection of planes and is therefore
a general irregular polyhedron. The facets of the Voronoi boxes correspond
in the dual graph to the Delaunay edges which connect the points of 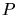 .
.
Figure 5.1:
Each Voronoi box associated with a point is differently
shaded. Two triangles 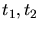 with their circumcenters
with their circumcenters
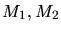 which are the vertices of the Voronoi boxes are depicted for
the correct Delaunay case and for the non-Delaunay case. Incorrect
Voronoi boxes which are derived from non-Delaunay triangles overlap.
which are the vertices of the Voronoi boxes are depicted for
the correct Delaunay case and for the non-Delaunay case. Incorrect
Voronoi boxes which are derived from non-Delaunay triangles overlap.
|
|
Combining this criterion for the three edges of a triangle and furthermore
for the four triangles of a tetrahedron leads to the following criteria for
Delaunay simplices. A Delaunay triangle is thereby the dual of a Voronoi
edge.
Figure 5.2:
The Delaunay edge (a) and Delaunay triangle (b) criteria.
|
|
Crit. 5.2 implies that an empty circumcircle is necessary
but not sufficient for Delaunay surface triangles in three dimensions.
This is the reason why a two-dimensional Delaunay Triangulation code is of
limited use to construct a three-dimensional Delaunay surface triangulation.
The Delaunay edge and Delaunay triangle criteria are depicted in
Fig. 5.2.
A Delaunay tetrahedron corresponds to a point in the Voronoi diagram, which
is the vertex of four5.1 incident Voronoi boxes.
A Delaunay tetrahedron must consist of Delaunay edges and
Delaunay triangles. The edge and triangle criteria are implicit, because the
existence of the  -dimensional sphere in Crit. 5.1 and
in Crit. 5.2 is guaranteed by the sphere in
Crit. 5.3.
-dimensional sphere in Crit. 5.1 and
in Crit. 5.2 is guaranteed by the sphere in
Crit. 5.3.
An anisotropic Delaunay Triangulation [20] can be
defined through a simple linear transformation. The empty circumcircle
criterion is applied in the transformed space and results in an empty
ellipse in the mesh space. The transformation must be allowed to
change over the domain to be practically useful. This leads to
difficulties in the grading of the mesh. For an extremely
inhomogeneous transformation the Delaunay Triangulation cannot be
applied in a consistent way and the excellent property to always
guarantee a valid tessellation without special consistency checks is
lost.



Next: 5.3 Algorithms for Constructing
Up: 5. Delaunay Triangulation
Previous: 5.1 Tetrahedralization of a
Peter Fleischmann
2000-01-20
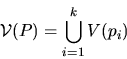
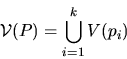
![\includegraphics [width=0.95\textwidth]{ppl/intu2.ps}](img215.gif)