


Next: 5.3.2 Sweepline
Up: 5.3 Algorithms for Constructing
Previous: 5.3 Algorithms for Constructing
The point set 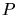 is recursively divided into halves until the subsets
contain a minimum number of points. These smallest sets of two or three
points can be linked yielding edges or triangles. The following conquer
step merges the subsets. Thereby the convex hull of a subset is traversed
and linked to the other subset. Re-connecting the points by e.g. flip
operations to satisfy the Delaunay criterion is equivalent to finding the
dividing polygonal chain between the Voronoi diagrams of the two subsets.
The dividing chain which consists of Voronoi edges can be constructed in
linear time which results in an overall
is recursively divided into halves until the subsets
contain a minimum number of points. These smallest sets of two or three
points can be linked yielding edges or triangles. The following conquer
step merges the subsets. Thereby the convex hull of a subset is traversed
and linked to the other subset. Re-connecting the points by e.g. flip
operations to satisfy the Delaunay criterion is equivalent to finding the
dividing polygonal chain between the Voronoi diagrams of the two subsets.
The dividing chain which consists of Voronoi edges can be constructed in
linear time which results in an overall 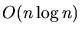 performance
[123].
performance
[123].
Peter Fleischmann
2000-01-20