Next: 5.3.3 Incremental Construction
Up: 5.3 Algorithms for Constructing
Previous: 5.3.1 Divide-and-Conquer
Sweepline methods form another general class of algorithms in computational
geometry as do the divide-and-conquer techniques.
For example in two dimensions a vertical line is swept from left to
right. The sweepline is halted at so called event locations where the status
of the sweepline is updated. Between events the sweepline does
not have to be halted because its status does not change.
In such a way the domain is partitioned into stripes which are sequentially
processed. The status of the sweepline and the type of events depend on the
application. For the construction of the Delaunay Triangulation such an
algorithm has been implemented by [46].
The boundary edges of the current (incomplete) state of the mesh are stored
in a tree data structure. An event occurs when the sweepline reaches a
point of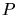 
or when it passes a circle formed by three adjacent vertices
of the current mesh boundary. New elements are created and the status of the
boundary edges is updated.
Peter Fleischmann
2000-01-20