



Next: 5.3.4 Incremental Search
Up: 5.3 Algorithms for Constructing
Previous: 5.3.2 Sweepline
An initial triangulation which covers the domain is constructed. For
example the bounding box is split into two triangles. The points of 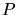 are
incrementally inserted into the triangulation. The triangle which contains
the inserted point is first located and then split. Two variations to this
algorithm exist. The topology around the inserted point can be updated by
flip operations to restore the Delaunay property [84].
Alternatively, all triangles whose circumcircles contain the inserted
point are removed and the resulting cavity is triangulated by linking
the inserted point to all vertices of the cavity boundary. This
simple linking scheme automatically guarantees the Delaunay property
of the new elements. The technique is referred to
as the Bowyer/Watson algorithm because it was simultaneously published
[186,21].
The cavity is star-shaped [123] because at
least one location exists (the location of the newly inserted point)
from which straight line segments can be drawn to all vertices of the
cavity without intersecting the cavity boundary.
are
incrementally inserted into the triangulation. The triangle which contains
the inserted point is first located and then split. Two variations to this
algorithm exist. The topology around the inserted point can be updated by
flip operations to restore the Delaunay property [84].
Alternatively, all triangles whose circumcircles contain the inserted
point are removed and the resulting cavity is triangulated by linking
the inserted point to all vertices of the cavity boundary. This
simple linking scheme automatically guarantees the Delaunay property
of the new elements. The technique is referred to
as the Bowyer/Watson algorithm because it was simultaneously published
[186,21].
The cavity is star-shaped [123] because at
least one location exists (the location of the newly inserted point)
from which straight line segments can be drawn to all vertices of the
cavity without intersecting the cavity boundary.
Peter Fleischmann
2000-01-20