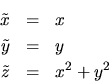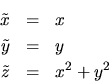Next: 5.4 Non-Uniqueness
Up: 5.3 Algorithms for Constructing
Previous: 5.3.4 Incremental Search
An 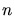 -dimensional Delaunay Triangulation can be deduced from a computation
of the convex hull in
-dimensional Delaunay Triangulation can be deduced from a computation
of the convex hull in 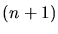 dimensions.
For example a two-dimensional Delaunay Triangulation of a point set
dimensions.
For example a two-dimensional Delaunay Triangulation of a point set 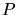 is
equivalent to the projection of the convex hull of a three-dimensional
point set
is
equivalent to the projection of the convex hull of a three-dimensional
point set 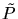 which is derived from
which is derived from 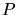 through a lifting
transformation [15,114].
through a lifting
transformation [15,114].
A detailed discussion of convex hull algorithms can be found in [123].
Peter Fleischmann
2000-01-20