



Next: 5.5 Boundary Integrity
Up: 5. Delaunay Triangulation
Previous: 5.3.5 Convex Hull
5.4 Non-Uniqueness
The definition of the Delaunay Triangulation for a given point set 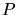 usually results in a unique triangulation/tetrahedralization of
usually results in a unique triangulation/tetrahedralization of 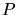 .
No two different triangulations/tetrahedralizations exist for the same
point set which both satisfy the Delaunay property.
However, degenerate subsets of points in
.
No two different triangulations/tetrahedralizations exist for the same
point set which both satisfy the Delaunay property.
However, degenerate subsets of points in 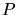 can be formed which lead to
non-uniqueness.
can be formed which lead to
non-uniqueness.
In such cases the length of a Voronoi edge or the area of a Voronoi facet
is zero. Hence, the corresponding Delaunay edges and facets are missing in
the dual graph, and non-simplicial polygons/polyhedra are formed. These can
be arbitrarily triangulated/tetrahedralized, because their topology remains
undefined by the Delaunay criterion.
In two dimensions such point sets are often called cocircular. However, one
should be aware that cocircularity in three dimensions refers to a more
specific degeneracy. It is useful to distinguish this special degenerate
case which only occurs in dimensions higher than two.
In fact a cocircular point set in three dimensions implies the existence of
two intersecting cospherical point sets. This is true as long as at least
one other point exists in each half space defined by the plane of the
cocircular point set.
Degenerate cases require specially enhanced algorithms to ensure a robust
Delaunay Triangulation engine. None of the above listed Delaunay algorithms
remain entirely unaffected. For the incremental search based algorithm the
consequences are discussed in detail in Section 6.4.3
and the implementation of a new and unconventional solution is presented.
A more typical approach to avoid degenerate cases is to apply perturbations
to the location of the points
[114,115,81]. However, this technique
is not as straightforward as it appears and other difficulties arise.
- It must be guaranteed that the perturbations destroy all
cospherical subsets and that they do not create new cospherical subsets.
- It can be shown that the number of sliver elements increases greatly
when cospherical point sets are perturbed. Additive noise does not affect a
random point set by nature, but the quality of a tetrahedralization of an
ortho-product point set is significantly reduced.
- If it is not permitted to dislocate certain points, e.g. vertices of
the boundary, the temporary additive noise must be removed when the
topology is set which is after the
triangulation/tetrahedralization. This is not easy because the
sliver elements which have been caused by the additive noise reach
zero volume when the points are re-positioned to their original location.




Next: 5.5 Boundary Integrity
Up: 5. Delaunay Triangulation
Previous: 5.3.5 Convex Hull
Peter Fleischmann
2000-01-20
![]() usually results in a unique triangulation/tetrahedralization of
usually results in a unique triangulation/tetrahedralization of ![]() .
No two different triangulations/tetrahedralizations exist for the same
point set which both satisfy the Delaunay property.
However, degenerate subsets of points in
.
No two different triangulations/tetrahedralizations exist for the same
point set which both satisfy the Delaunay property.
However, degenerate subsets of points in ![]() can be formed which lead to
non-uniqueness.
can be formed which lead to
non-uniqueness.