5.5.1 Constrained Delaunay Triangulation

A constrained Delaunay Triangulation (CDT) [155] is depicted in Fig. 5.3-b. The boundary edges are preserved and not split into smaller edges by avoiding the insertion of additional points. Their presence in the CDT is ensured through local modifications where Delaunay edges are removed or flipped. The resulting Delaunay Triangulation is said to be constrained by the boundary. Elements near the boundary are not guaranteed to satisfy the Delaunay criterion. Even though the smallest sphere criterion (Crit. 3.1) for boundary edges is stronger than the Delaunay criterion, it can paradoxically be of advantage for meshing applications to use CDT. The reason lies in the for meshing applications different perception of proximity as can be seen in Fig. 5.4. If one defines as medium for visibility the mesh elements, the point $P$ in Fig. 5.4 is invisible from the edge $e$. Therefore, for the mesh element adjacent at edge $e$ the point $P$ can be ignored and the smallest sphere criterion is in this sense fulfilled, although the edge $e$ is not even a Delaunay edge. If the boundary depicted in the figure were an interface between the meshes of two regions, the point $P$ would certainly inflict the smallest sphere criterion of edge $e$, and the Delaunay criterion for the interface edges would not be sufficient but necessary.

Figure 5.4: A constrained Delaunay Triangulation with a non-Delaunay edge $e$. The point $P$ does not affect edge $e$. The half of the smallest sphere which lies inside the mesh is highlighted.

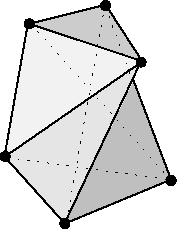
Contrary to the two-dimensional case a constrained Delaunay Triangulation does not exist a priori in three dimensions. Constellations of boundary facets exist which cannot be tetrahedralized without the insertion of additional points on the boundary. In other words no tetrahedralization can be found regardless of Delaunay criteria which allows the preservation of the boundary facets. An example of such a constellation is the twisted prism or Schönhardt polyhedron [149] which requires the insertion of at least one additional vertex (Fig. 5.5). No tetrahedron can be attached to the bottom facet with any of the top three vertices as fourth point without that it intersects one of the diagonal side edges.

Figure 5.5: An untetrahedralizable twisted prism where the diagonals of the three side facets almost intersect.

This leads to the important question how to determine whether or not additional vertices are required to tessellate a general polyhedron. Unfortunately it has been shown that this problem is NP-complete^5.2[136,137,14]. A condition for the existence of a higher dimensional CDT is examined in [163]. An important question is how to insert the additional vertices to guarantee a tessellation without further refinement of the boundary.