| location |
a space defined by a set of coordinates |
| vertex |
a zero-dimensional part of a higher dimensional entity,
e.g. part of a geometry, a polygon, or polyhedron |
| n-simplex |
(n+1) affinely independent vertices |
| point |
a zero-simplex |
| edge |
a one-simplex |
| triangle |
a two-simplex |
| tetrahedron |
a three-simplex |
| node |
not a point, but part of a tree data structure |
| facet |
a two-dimensional entity, e.g. a polygon |
| face |
the verb as in ``facing a direction'' |
| non-planar |
curved, but mostly used as short form for
piecewise-planar |
| topology |
the connectivity of a set of points where adjacency
is given by the edges regardless of the location of the points |
| boundary |
(n-1)-dimensional topology in 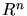 |
| grid |
n-dimensional structured topology in 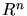 ,
numerical grid ,
numerical grid |
| mesh |
n-dimensional unstructured topology in 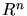 |
| surface mesh |
(n-1)-dimensional unstructured topology in
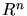 |
| triangulation |
a simplicial complex [118] where the
highest order element
is a 2-simplex in 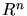 |
| tetrahedralization |
a simplicial complex where the highest
order element is
a 3-simplex in 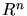 |
| Triangulation |
special triangulation or tetrahedralization as
for example in ``Delaunay Triangulation'' or ``Steiner
Triangulation'',
independent of the order of the
simplices |
| boundary consistent |
incorporating the boundary, as opposed to
intersecting or overlapping |
| boundary-fitted |
nicely aligned with the boundary and not just
boundary
consistent |
| boundary conforming |
This term is avoided because it is
sometimes used in different ways throughout literature, e.g. as boundary
consistent or as boundary-fitted. |