Spin-Orbit Coupling

2.2 Spin-Orbit Coupling

Figure 2.2: Bloch sphere with different qubit states corresponding to the axes is shown. The position of an arbitrary state (χ) can be uniquely represented by the polar (Θ) and the azimuthal angles (Φ).

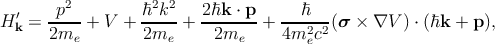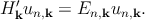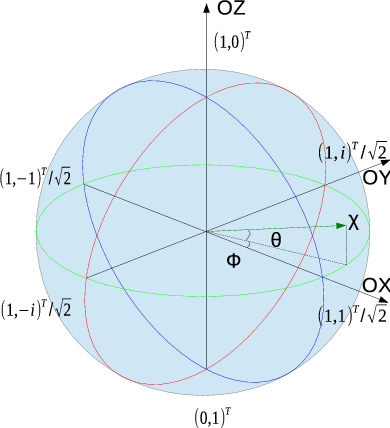
Classically electrons can be thought of a spinning ball of charge, and the correlated angular momentum is called spin. The experiment from [23] confirmed the quantization of the electron spin into two orientations which paved the way of quantum mechanics of spin. Theoretically, a two-state quantum system (e.g. electron spin) is a system which can exist in any quantum superposition of two independent and physically distinguishable states. The actual state of the electron spin can geometrically be represented by any point in the Bloch sphere (Figure 2.2). Through several experiments it has been shown that the electrons’ spin can have only two opposing projections on a fixed axis, and hence only two independent measurable states. These two orthonormal eigenstates (basis) are postulated as |↑⟩ and |↓⟩ where,

[ ] 1 |↑⟩ → 0 ,

(2.16)

[0] |↓⟩ → . 1

(2.17)

Any quantum state |χ⟩ represented by a point on the Bloch sphere (defined through the polar Θ and the azimuthal Φ angles) can always be expressed as a superposition of the basis vectors |↑⟩ and |↓⟩, where the coefficient or amount of each basis vector is a complex number. Since only the relative phase between the coefficients of the two basis vectors has any physical meaning, one can take the coefficient of |↑⟩ to be real and non-negative. From postulates of quantum mechanics the total probability of the system has to be one, and thus ⟨χ|χ⟩=1. Given this constraint, the quantum state |χ⟩ can be expressed as [131]

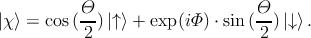Θ Θ |χ⟩ = cos (--)|↑⟩ + exp (iΦ) ⋅ sin (-)|↓⟩. 2 2

(2.18)

where 0 ≤ Θ ≤ π and 0 ≤ Φ < 2π.

The interaction of the electron spin with the electric field (via the associated magnetic field in the electrons rest frame) and hence the electron’s motion in a crystal is called the spin-orbit interaction. This can be represented by the Hamiltonian [128],

ℏ HSO = ---2-2[∇V × p ] ⋅ σ. 4m ec

(2.19)

Here, c is the speed of light at vacuum, m_e is the electron rest mass, V is the periodic potential, and σ = (σ_x,σ_y,σ_z) is the spin vector in the Pauli matrices basis.

The k ⋅ p Method with Spin-Orbit Coupling

In order to include the spin-orbit coupling, one has to add Equation 2.19 to Equation 2.8 to obtain

p2 ℏ Hk = 2m--+ V + 4m2c2-[∇V × p] ⋅ σ. e e

(2.20)

Analog to the derivation shown in in the section 2.1.6, one has to apply a Bloch ansatz to the Schrödinger equation with the modified Hamiltonian from Equation 2.20 [132] to derive the equation for the k ⋅ p method analysis.

2 2 2 H ′k = -p-- + V + ℏ-k--+ 2ℏk--⋅ p +---ℏ--(σ × ∇V ) ⋅ (ℏk + p ), 2me 2me 2me 4m2ec2

(2.21a)

′ H kun,k = En,kun,k.

(2.21b)

With the notation

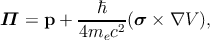ℏ Π = p + -----2(σ × ∇V ), 4mec

(2.22)

the above equation turns out to be

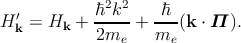ℏ2k2 ℏ H ′k = Hk + -----+ ---(k ⋅ Π ). 2me me

(2.23)

[next] [prev] [prev-tail] [front] [up]