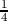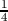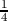3.1 Silicon Lattice

The Miller indices, denoted as h, k, and l, are a symbolic vector representation for the orientation of atomic planes and directions in a crystal lattice. Defining three lattice vectors forming the lattice axes, any crystal plane would intersect the axes at three distinct points. The Miller indices are obtained by taking the reciprocal of the intercepted values. By convention, negative indices are written with a bar over the indices. The adopted nomenclature is as described below [139].

• A direction is represented by [hkl],
• the equivalent directions are denoted by <hkl>,
• a plane with the normal vector [hkl] is represented by (hkl), and
• the equivalent planes are denoted by {hkl}.

The crystal structure of silicon is classified under the diamond structure [139], and thus has two atoms in a primitive cell. Germanium, and carbon are further examples of a diamond structure lattice. On the contrary, the III-V semiconductors (GaAs, AlAs, InAs, InP etc.) are of zinc blende type. The crystal lattice of silicon can be represented as two penetrating face centered cubic lattices (fcc) with the cube side a=0.543nm as portrayed in Figure 3.1. The structure is visualized as a tetrahedron with four vertices of the first fcc lattice at (0,0,0), (a/2,0,0), (0,a/2,0) and (0,0,a/2) and an additional atom added to the center of this tetrahedron. The additional atom is displaced by a(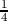,,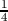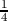) with respect to the original fcc lattice. One unit cell of silicon consists of eight atoms, where their distribution with reference to Figure 3.1 is described as below.

• Each of the eight atoms (A^′, pertaining to the first fcc lattice) on the corners are shared among each cell, thus counting equivalent one atom inside the cell (gray colored),
• each of the six atoms (A^′) on the faces are shared among two cells, thus counting three more atoms inside the shell (red colored), and
• four atoms (A^′′, pertaining to the second fcc lattice) rest completely inside the cell (blue colored).