2.3.3.6 Current Source

The constitutive relation for an ideal current source is given as I = I₀(t). The current can be arbitrarily time-dependent and several common curve shapes have been implemented. However, no dependence on solution variables is allowed as this would result in a voltage or current controlled source (see Section 2.3.3.8 and Section 2.3.3.9). The stamp is given as

yx, y	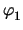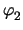$\varphi_{1}^{}$	$\varphi_{2}^{}$	f
n1			I
n2			- I

The sign of the current is different as compared to the passive elements as it is defined to flow out of the source. Generalizing the branch relation to I = I₀(t) - V ^. G, that is to a current source with shunt resistance, gives the following stamp

yx, y	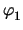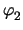$\varphi_{1}^{}$	$\varphi_{2}^{}$	f
n1	G	- G	I
n2	- G	G	- I

which is of course the superposition of an ideal current source with an ideal conductor.