B2. Real Device Classes

Figure B.1: Class hierarchy within the Algorithm Library and definition of the communication interface to the simulator.

Class hierarchy is shown in Fig. B.1 Each instance is created completely dynamically. This is in contrast to e.g., SPICE where all necessary information is taken from statically allocated tables which is of course faster. However, the overhead is minimal and occurs only during initialization but the device can be optimally configured because only those parameters and keywords are added which are really needed. This is done in the init method where each device must declare its nodes and the keywords to configure the device model. Nodes correspond to solution variables and the number of nodes determines the size of the partial Jacobian matrix allocated for the device. A purely electric, two-terminal device would register two nodes and would in turn get a 2 x 2 partial Jacobian matrix Y assigned. For purely voltage controlled devices Y is of admittance form. Available node types are:

• Normal nodes which provide a connection to a circuit node voltage.
• Internal nodes which are unique and cannot be shared between different devices but can be used to build internal subcircuits. A typical application is the addition of internal series resistances.
• Branch current nodes which introduce a new branch current into the equation system.
• Thermal nodes are the analog to normal nodes and provide a connection to a thermal circuit node.
• Internal thermal nodes can be used to build internal thermal circuits.
• Thermal branch currents introduce a new thermal branch current (heat flow) into the equation system.

The init method of a simple diode is shown in the following.

class MmxDiode : MmxDevice
{
   Param<double> Is, rs, V, I, T, gm;
   ...
}

vBoolean MmxDiode::init()
{
  addKeyword(Is, "Is", "Current");
  addKeyword(rs, "rs", "Resistance");

  readKeywords();

  addNode("A");         // Anode
  addNode("C");         // Cathode

  addThermalNode("T");

  if (rs > 0.0)
     addInternNode("intern");

  addOutput(V,  "V",  "Potential");
  addOutput(I,  "I",  "Current");
  addOutput(T,  "T",  "Temperature");
  addOutput(gm, "gm", "Conductance");

  return vTRUE;
}

The diode model implements the simple equations

$$\left(\vphantom{\exp\left(\frac{\mathrm{q}\cdot V_d}{\mathrm{k_{B}}\cdot T}\right) - 1}\right. \left(\vphantom{\frac{\mathrm{q}\cdot V_d}{\mathrm{k_{B}}\cdot T}}\right. 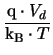{\frac{\mathrm{q}\cdot V_d}{\mathrm{k_{B}}\cdot T}} \left.\vphantom{\frac{\mathrm{q}\cdot V_d}{\mathrm{k_{B}}\cdot T}}\right) \left.\vphantom{\exp\left(\frac{\mathrm{q}\cdot V_d}{\mathrm{k_{B}}\cdot T}\right) - 1}\right)$$ I_d = (B1)

P_d = I_d ^. V_d   . (B2)

In addition, a series resistance r_s can be added. This is done via the keyword rs which is registered to be of quantity type "Resistance". Quantity types are available for many different physical quantities and provide access to SI-units, internal units, communication units and their respective scaling factors. Three different unit types are necessary because of the following reasons

• SI-units are used in all device models. All keywords, input and output parameters will be provided in SI-units.
• Properly scaled internal units are used in the simulator core of MINIMOS-NT to assure a stable equation system.
• Communication units are used for the communication with the user. They are the default units when reading values from the input deck if not overwritten there. When writting information to e.g., log-files quantities are written in communication units.

E.g., for concentrations the SI-units are m^-3, the internal units are 10¹⁹cm^-3 while the communication units are cm^-3. These quantity types guarantee consistent handling of the above units.

After registering the keywords with calls to the member function addKeyword the member function readKeywords is called which reads the values for this instance from the input deck. Then the two device nodes for the anode "A", the cathode "C" and the thermal node "T" are registered. Only when the user specified a series resistance an internal node is needed which is dynamically added. Finally, the instance output parameters are registered via calls to the member function addOutput. All parameters registered this way are written to the log-file as simulation result. In addition, they can be inquired within the input deck using the output function. The init method is called from the default constructor. For each iteration of the Newton method the evaluate method is called. Before each call Y and rhs are cleared and x initialized with proper values from the last solution. Furthermore, a special vector called solv is initialized. It states which quantities are really solved for to speed up calculation. The evaluate method is expected to fill in Y, rhs and the instance output parameters. In the following, a version stripped of all numerical subtleties is shown

vBoolean MmxDiode::evaluate()
{
  T = x[nT];
  V = x[n1] - x[n2];

  vDouble VTinv = Const.q / (Const.k * T);
  vDouble Ix = Is * Exp(V * VTinv);
  I  = Ix - Is + V * gmin;
  gm = Ix * VTinv + gmin;

  Y[n1][n1] =  gm;
  Y[n2][n2] =  gm;
  Y[n1][n2] = -gm;
  Y[n2][n1] = -gm;

  rhs[n1] = -I;
  rhs[n2] =  I;

  if (solv[nT])
  {
     vDouble dIdT = - V * gm / T;

     Y[n1][nT] =   dIdT;
     Y[n2][nT] = - dIdT;
     rhs[nT]   = I * V;
  }

  return vTRUE;
}

An additional feature of the Algorithm Library allows for interpreted models. From the users point of view these model are indistinguishable from built-in models except being slower by about a factor of 2. When they are compiled, no noticeable difference in performance was found. This is because the evaluate method can be very easily mapped to C++ due to the similarity of MDL to C++. Providing the proper inheritance information and keywords is more complicated but fortunately only necessary once during initialization.

The following example shows the diode model as implemented in MDL syntax.

NewModel MdlDiode : Device
{
  Local
  {
     Parameter<double>  VTinv, Ix, dIdT;
  }
 
  construct
  {
     key["Is"] = {{ Quantity Current    }};
     key["rs"] = {{ Quantity Resistance }};

     call readKeywords;

     node["n1"] = {{ Voltage }};
     node["n2"] = {{ Voltage }};

     if (rs > 0)
       node["nT"] = {{ Thermal }};

     output["I"]  = {{ Quantity Current     }};
     output["V"]  = {{ Quantity Voltage     }};
     output["T"]  = {{ Quantity Temperature }};
     output["gm"] = {{ Quantity Conductance }};

     call addNodesAndOutput;
  }

  evaluate
  {
     T = :x[nT];
     V = :x[n1] - x[n2];

     VTinv = Const.q / (T * Const.k);
     Ix = Is * exp(V * VTinv);
     I  = Ix - Is + V * gmin;
     gm = Ix * VTinv + gmin;

     :Y[n1][n1] =  gm;
     :Y[n2][n2] =  gm;
     :Y[n1][n2] = -gm;
     :Y[n2][n1] = -gm;
   
     :rhs[n1] = -I;
     :rhs[n2] =  I;

     if (solv[nT])
     {
        dIdT = - V * gm / T;
   
        :Y[n1][nT] =   dIdT;
        :Y[n2][nT] = - dIdT;
        :rhs[nT]   = I * V;
     }
  }     
}

In the model constructor three lists are available to register keywords, nodes, and output parameters. For each argument of these lists, a local parameter is created which can be used in all other methods. The keyword list is the same as for the physical models. The node list registers the external and internal nodes of the device model. External nodes are Voltage and Temperature for voltage and temperature nodes, respectively. Internal nodes of type VoltageInternal can be created which are not visible from outside. Branch currents and heat flows can be registered using Current and HeatFlow, respectively.

As interface parameters the solution of the previous iteration (x), the partial Jacobian matrix (Y) and the right hand side of the current iteration (rhs) are available. They are distinguished from the local parameters by the colon. The solution vector can be used to inquire the potentials and temperatures at the circuit nodes and the branch currents and heat flows of the device. The model must calculate the partial Jacobian matrix and the right hand side for the current operating point. This is done in the evaluate method.