The component of the current which is caused by the electric field is called drift
current. From the macroscopic point of view the current density and the electric field are
related by OHM's law
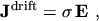 |
(2.20) |
where 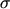 is the electrical conductivity. It is in general a tensor but can be assumed
as a scalar in most semiconductors2.3.
is the electrical conductivity. It is in general a tensor but can be assumed
as a scalar in most semiconductors2.3.
From the microscopic point of view the current density is made up by the moving carriers
 |
(2.21) |
where
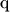 is the elementary charge,
is the elementary charge, 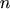 and
and 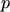 are the electron and hole concentrations,
respectively, and
are the electron and hole concentrations,
respectively, and
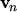 and
and
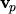 are the mean
velocities of electrons and holes, respectively. The electric field accelerates the carriers,
but due to various scattering mechanisms the velocity of the carriers is limited:
are the mean
velocities of electrons and holes, respectively. The electric field accelerates the carriers,
but due to various scattering mechanisms the velocity of the carriers is limited:
where 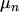 and
and 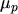 are the mobility of electrons and holes, respectively. By inserting
these two equations into eqn. (2.21)
are the mobility of electrons and holes, respectively. By inserting
these two equations into eqn. (2.21)
 |
(2.24) |
and comparing eqn. (2.24) with eqn. (2.20) and eqn. (2.19) the following
relations are obtained:
and for the conductivities:
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF