For the sake of brevity, a one-dimensional investigation will be given. The results can be
extended straightforwardly to higher dimensions [8, p.150]. Considering a
set of grid points 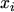 the spacing is defined by
the spacing is defined by
 |
(3.1) |
Fig. 3.2 shows the notation used.
Figure 3.2:
Three adjacent grid points together with some notational abbreviations used in the
derivation.
|
![\includegraphics[width=.7\textwidth]{eps/FiniteDifferenceMethod.eps}](img722.png) |
For the discretization of the flux equations the derivatives in-between the grid points are
important. Therefore a TAYLOR series expansion [47, p.415] around
the mid point
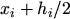 is considered
is considered
To get an expression for the first order derivatives the series up to the order 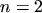 is evaluated at
is evaluated at 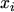 and
and 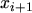
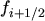 can be eliminated by subtracting the two equations and thus the first order
derivative becomes
can be eliminated by subtracting the two equations and thus the first order
derivative becomes
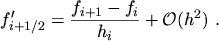 |
(3.6) |
For the second order derivatives the TAYLOR series expansion around 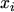
 |
(3.7) |
is evaluated up to the order 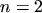 at
at 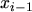 and
and 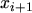
and by eliminating 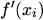 the second order derivative is found to be
the second order derivative is found to be
 |
(3.10) |
No assumption about the uniformity of the grid has been made during the derivation of
eqn. (3.6) and eqn. (3.10), so the estimated
truncation errors are valid for a non-uniform grid. If a uniform grid spacing is assumed, the
truncation error will be of order
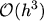 in eqn. (3.6) and
in eqn. (3.6) and
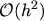 in eqn. (3.10) [8, p.153].
in eqn. (3.10) [8, p.153].
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![\includegraphics[width=.7\textwidth]{eps/FiniteDifferenceMethod.eps}](img722.png)
![]() is considered
is considered

![]() is evaluated at
is evaluated at ![]() and
and ![]()
![]()

![]() in eqn. (3.6) and
in eqn. (3.6) and
![]() in eqn. (3.10) [8, p.153].
in eqn. (3.10) [8, p.153].