The current density is discretized by a scheme which is frequently referred to as
SCHARFETTER-GUMMEL discretization [51]. The extension of the
discretization to the flux equations stemming from the higher order moments of
BOLTZMANN's equation is not beyond controversy, so different approaches can be
found in the literature. In [23] it is assumed that the electron concentration is a
known function of exponential shape. This strategy is refined in [37] where the
variation of the electron concentration obtained from the discretization of the current
density equation is used for discretizing the energy flux density. This text will follow the
approach presented in [31], which is an extension of [52] and [53],
where a generalized expression for the fluxes is used and no assumption about the variation of
the carrier concentration is made.
By rewriting the flux equations (2.188) to (2.190)
a common functional form can be recognized. Therefore a general flux equation is
introduced
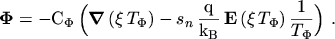 |
(3.37) |
The meanings of the generalized density 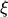 and temperature
and temperature 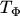 is found by inspection:
is found by inspection:
By projecting eqn. (3.37) onto a grid line a one-dimensional differential equation
is obtained
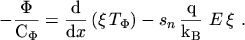 |
(3.41) |
To solve this equation the following assumptions have been made:
- constant general flux
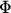 ,
,
- constant electric field
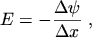 |
(3.42) |
- linear variation of the general temperature
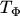
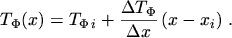 |
(3.43) |
The solution of eqn. (3.41) is found by multiplication with an integrating
factor 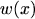 and by sub-sequentially comparing the coefficients of the resulting equation
with the total derivative of the product
and by sub-sequentially comparing the coefficients of the resulting equation
with the total derivative of the product
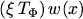 :
:
Comparing the coefficients leads to
This equation can be solved for the integrating factor 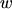 , taking into account the
assumptions (3.42) and (3.43):
, taking into account the
assumptions (3.42) and (3.43):
Inserting the integrating factor into eqn. (3.44)
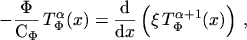 |
(3.50) |
and assuming that the flux 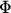 is constant between two grid points,
eqn. (3.50) can be integrated from
is constant between two grid points,
eqn. (3.50) can be integrated from 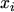 to
to 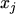
Commonly eqn. (3.52) is rewritten using the BERNOULLI
function
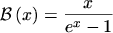 |
(3.53) |
Beginning with
and using the abbreviations
the flux equation can be written as
or using the BERNOULLI function as
The concept of assuming a constant flux density was first presented by SCHARFETTER
and GUMMEL in the appendix of [51, p.73]. The assumption of a
linear variation of the generalized temperature 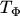 by eqn. (3.43) can be
interpreted as a straightforward extension of the SCHARFETTER-GUMMEL scheme.
by eqn. (3.43) can be
interpreted as a straightforward extension of the SCHARFETTER-GUMMEL scheme.
An advantage of using BERNOULLI functions in the flux equations is that
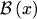 is well defined at
is well defined at 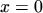 .
.
Inserting the abbreviations (3.38) to (3.40) used for 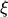 and
and 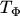 yields the discretized flux equations
yields the discretized flux equations
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![]() and by sub-sequentially comparing the coefficients of the resulting equation
with the total derivative of the product
and by sub-sequentially comparing the coefficients of the resulting equation
with the total derivative of the product
![]() :
:
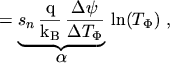
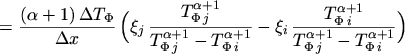
![]() by eqn. (3.43) can be
interpreted as a straightforward extension of the SCHARFETTER-GUMMEL scheme.
by eqn. (3.43) can be
interpreted as a straightforward extension of the SCHARFETTER-GUMMEL scheme.
![]() is well defined at
is well defined at ![]() .
.
![]() and
and ![]() yields the discretized flux equations
yields the discretized flux equations