In the channel of state-of-the-art MOSFET devices, strong gradients of the electric
field occur. These highly non-uniform field distributions give rise to distribution functions
which deviate significantly from the MAXWELLian distribution. However, the
standard energy transport models are based on the assumption of a heated MAXWELLian
distribution. Even in a homogeneous semiconductor the distribution function cannot be described properly by a
heated MAXWELLian distribution at high field values. Fig. 5.9 shows the
distribution function in homogeneous silicon with a bulk doping of
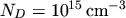 . The
deviation from the MAXWELLian shape is obvious, which would appear as a straight
line due to the logarithmic scale.
. The
deviation from the MAXWELLian shape is obvious, which would appear as a straight
line due to the logarithmic scale.
Figure 5.9:
Distribution function in bulk for different electric field values.
|
 |
The energy flux equation (2.162) contains the moment of
fourth order of the distribution function,
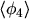 :
:
 |
(5.36) |
To close the set of energy transport equations,
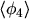 needs to be expressed as a function of
lower order moments. Assuming a MAXWELLian distribution function gives
needs to be expressed as a function of
lower order moments. Assuming a MAXWELLian distribution function gives
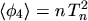 , whereas a non-MAXWELLian distribution function can be characterized by
, whereas a non-MAXWELLian distribution function can be characterized by
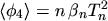 , using a non-MAXWELLian parameter
, using a non-MAXWELLian parameter
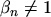 .
.
Regions of the channel where the high energy tail is underpopulated (points B, C, D, E in
Fig. 5.6, Region II in Fig. 5.8) are characterized by
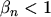 .
.
The non-MAXWELLian effects turned out to be important for SOI
simulations. It is believed that standard energy transport SOI simulations yield anomalous
results mainly because these effects are neglected. The problem is that in the energy transport
framework there is no information about the non-MAXWELLian parameter 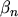 . In
Chapter 6, several attempts are made to estimate this additional
information.
. In
Chapter 6, several attempts are made to estimate this additional
information.
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![]() :
:
![]() .
.
![]() . In
Chapter 6, several attempts are made to estimate this additional
information.
. In
Chapter 6, several attempts are made to estimate this additional
information.