6.3 Summarizing the Models

$\displaystyle J_{n, \, l}$	$\displaystyle = \mu_n \, \mathrm{k}_\mathrm{B}\, \Bigl( \ensuremath{\partial_{l... ...T_{ll} \bigr)}+ \frac{\mathrm{q}}{\mathrm{k}_\mathrm{B}} \, E_l \, n \Bigr) \ ,$	(6.16)
$\displaystyle S_{n, \, l}$	$\displaystyle = - \frac{5}{2} \, \frac{\mathrm{k}_\mathrm{B}^2}{\mathrm{q}} \, ... ...athrm{k}_\mathrm{B}} \, E_l \, n \, \frac{3 \, T_n + 2 \, T_{ll}}{5} \Bigr) \ .$	(6.17)

The carrier temperature

defined by eqn. (2.94) is a measure of average carrier energy. The diagonal component of the temperature tensor is given by $\mathrm{k}_\mathrm{B}\, T_{ll} = \ensuremath{\langle v_l \, p_l \rangle}$ . Off-diagonal components are neglected. The solution variable is still the carrier temperature

, whereas the tensor components and the fourth order moment are modeled empirically as functions of

(enqs. (6.3) and (6.15)):

$\displaystyle \gamma_\nu$	$\displaystyle = \gamma_{0\nu} + \bigl( 1 - \gamma_{0\nu} \bigr) \, \exp \Bigl( ... ...}} \Bigr)^2 \Bigr) \ , \textcolor{lightgrey}{.......}\nu = \parallel, \perp \ ,$	(6.18)
$\displaystyle \beta_{n}$	$\displaystyle = \beta_0 + \bigl( 1 - \beta_0 \bigr) \, \exp \Bigl( - \Bigl( \frac{T_n - T_\mathrm{L}}{\mathrm{T_{ref, \beta}}} \Bigr)^2 \Bigr) \ .$	(6.19)

$\displaystyle T_{\nu} = \gamma_\nu \, T_n \ , \textcolor{lightgrey}{.......}\nu = \parallel, \perp \ .$

(6.20)

$\displaystyle T_{ll}$	$\displaystyle = T_\parallel \, \cos^2 \varphi + T_\perp \, \sin^2 \varphi \ ,$	(6.21)
$\displaystyle \varphi$	$\displaystyle = \arccos ( \ensuremath{\boldsymbol{\mathrm{e}}}_l \ensuremath{\cdot}\ensuremath{\boldsymbol{\mathrm{e}}}_J ) \ .$	(6.22)

The graphs of the functions of eqns. (6.18) and (6.19) are displayed in Fig. 6.7.

**Figure 6.7:** Shape of the functions used to model $\gamma _\nu$ and $\beta _n$ . $\gamma _0$ and $\beta _0$ have been chosen to be .
$\includegraphics{gpfigure/Functional_Shape.color.eps}$

Both functions assume unity for $T_n=T_\mathrm{L}$ and an asymptotic value for large

. The exact shape of the transition between these two regions is only of minor importance and mainly affects the numerical stability. Therefore the transition should not be too steep. $\mathrm{T_{ref}} = 600 \, \mathrm{K}$ appeared to be an appropriate value. Parameter values for $\gamma_{0\nu}$ , $\beta _0$ , and $\mathrm{T_{ref}}$ can be roughly estimated from Monte Carlo simulations of one-dimensional

test structures (Tbl. 6.1).

Table 6.1: Parameter values estimated from Monte Carlo simulations.

$\gamma_{0\parallel}$	$\gamma_{0\perp}$	$\beta _0$	$\mathrm{T_{ref, \gamma_\parallel}}$	$\mathrm{T_{ref, \gamma_\perp}}$	$\mathrm{T_{ref, \beta}}$
			$600 \, \mathrm{K}$	$600 \, \mathrm{K}$	$600 \, \mathrm{K}$

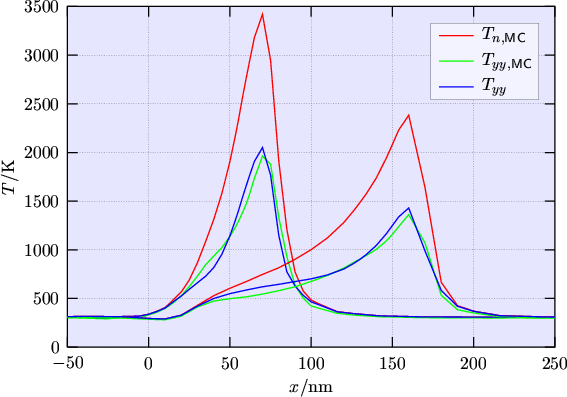
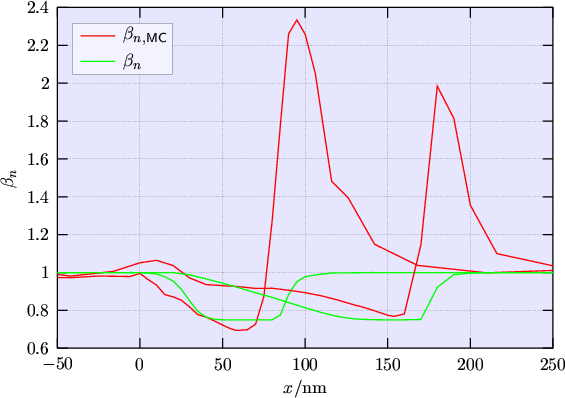
Monte Carlo results for the anisotropic temperature in a MOSFET are shown in Fig. 6.8 and Fig. 6.9 in comparison with the analytical models. Fig. 6.8 indicates that values for the anisotropy parameter can be as low as $\gamma _{0y} = 0.6$ . Values close to $\beta _0 = 0.75$ for the non-MAXWELLian parameter in the channel region can be estimated from Fig. 6.9. These parameters show only a weak dependence on doping and applied voltage.

**Figure 6.8:** Monte Carlo simulation of a $90 \hspace {.35ex} \textrm {nm}$ and a $180 \hspace {.35ex} \textrm {nm}$ MOSFET (Device 3 with different gate-lengths) showing the -component of the temperature tensor at the surface compared to the temperature $T_{n, \textsf {MC}}$ from the mean energy. The analytical model for $T_{yy}$ uses $\gamma _{0y} = 0.6$ .
$\includegraphics{gpfigure/Tn_Tyy_MOS.color.eps}$

**Figure 6.9:** Monte Carlo simulation of a $90 \hspace {.35ex} \textrm {nm}$ and a $180 \hspace {.35ex} \textrm {nm}$ MOSFET (Device 3 with different gate-lengths) showing the normalized moment of fourth order $\beta _{n, \textsf {MC}}$ at the surface compared to the analytical model for $\beta _n$ with $\beta _0 = 0.75$ .
$\includegraphics{gpfigure/beta_MOS.color.eps}$


Previous: 6.2.3 Inhomogeneous Case Up: 6. Modeling and Application Next: 6.4 Using the Modified Energy Transport Model