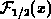
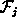 til 1982)
til 1982)
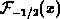
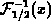
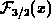
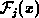




Fermi integrals and their inverse functions cannot be analytically presented in finite form, with exception of a few special cases. The approximation of these functions is covered rather extensively in literature. The approaches ranges from crude, but simple formulas with proper asymptotic behaviors [475][416], over the classical approximations reviewed in comprehensive work [35], to novel general expressions of very high accuracy [147][90][89].
Most of the published works on this subject are listed in the following table:
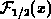
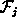 til 1982)
til 1982)
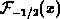
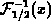
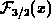
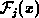
In calculations carried out in this work, we employed simple expressions
We observed that these expressions are sufficiently accurate for all our applications, except for the calculations close to flat-band condition in the gate, where a better approximation for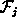 ought to be applied to
calculate
ought to be applied to
calculate 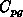 .
.